この解を y = f(x) とおくと、

画像
となります。
(2) y(0) = 1 + A = 2 なので A = 1
　　この解を y = g(x) とおくと、

画像
となります。

(3) y = f(x) を微分すると

画像
　f'(x) = 0 となるのは x = 0 。
　f'(−1) ＜ 0, f'(1) ＞ 0 なので f(0) は極小値です。
　さらに y(−∞) = 1,　y(+∞) = 1 です。

　また g(x) = −f(x) + 2 ですから、f(x) のグラフを x 軸で上下折り返して y 軸方向に 2 を加えればよいことがわかります。以上より、グラフの概形はまとめて次のようになります。

　

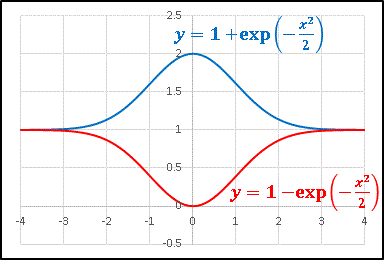
　ちなみに A = 0 のとき、すなわち y = 1 も解曲線の１つであり、微分方程式を満たしていること