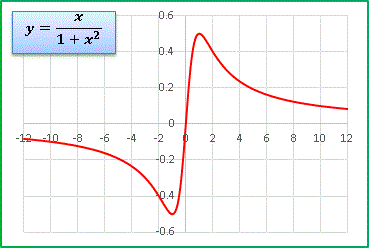
奇関数ですね。 x < 0 で負の値をとるようになります。
　この関数にさらに x をかけると再び偶関数になりますが ......

　

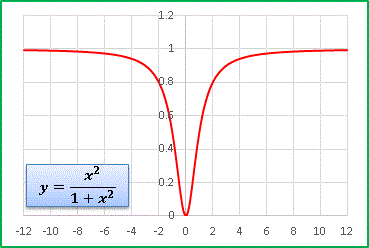
　今度は原点で谷を作ります。 [1] が原点で最大値 1 をとる関数ですから、 x 2 をかけると原点近傍は y < 1 となります。漸近線は y = 1 です。次はこの関数の分子に x の項を加えてみます：

　

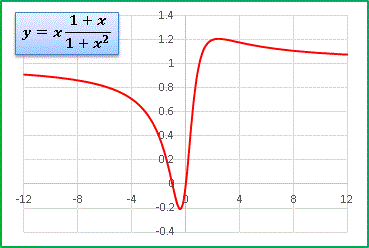
　対称性は失われますが、やはり漸近線は y = 1 です。
　分子・分母ともに２次式であることに変わりはないからです。

　最後に [1] に sinx と xsinx をかけて奇・偶の周期関数を作ってみます：