ての種類の数を含みます。ですからあらゆる数は「これは複素数だね」と言えば、正解と言えば正解なのですけど、やっぱり物事はもう少し細かく分類しておかないと、これから色々と不便です。

　そこでまず実数を「有理数」と「無理数」とに分けます。

　「有理数」とは 1/2, 3/7 のように分数で表せる数のことです。別の言い方をすれば、1：2, 3：7 のように比で表せる数ということです。

　では無理数とは何でしょうか？
　一辺の長さが１の正方形を書いてみます。そして対角線を引きます。この対角線の長さを求めてみましょう。小学校でやる図形の問題みたいですよね。でもこれ、簡単なようでいてとっても難しいのです。もう少し先のお話の先取りになりますが、少しだけ『ピタゴラスの定理』を使ってみましょう。

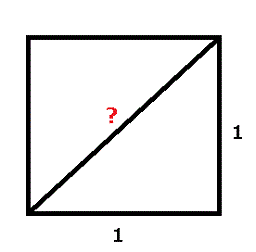
直角三角形の斜辺の長さを x, その他の２つの辺の長さを a, b とすると、

x 2 = a 2 + b 2
が成り立つことが知られています。今は a = b = 1ですから、とても簡単な形となって、

x 2 = 2
となりますね。つまり「２乗して 2 となる数を求めなさい」という問題になります。さきほどの虚数の場合と比べると、「何となくできそうだな」と思えますよね。ちょっと探してみましょう。1 と 2 の間にあるはずですから、x = 1.5 としてみましょうか。

1.5 × 1.5 = 2.25
ちょっと大きすぎました。少し値を小さくして x = 1.4 としてみます。

1.4 × 1.4 = 1.96
　惜しいですね