en を n! で割った数列

画像
が n → ∞ で 0 に収束することは微積分で有名な定理（というよりほとんど自明の事実）です。 n! が強すぎるので収束はとても早いです。グラフに描いてみると次のようになります。

　

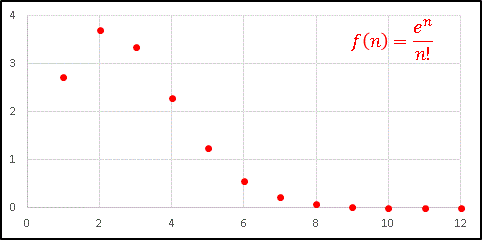
　n = 10 あたりをとれば、ほぼ 0 に収束したと言ってもいいぐらいです。

指数関数をガンマ関数で割ります　f(n) を実数関数 f(x) に拡張するには、ガンマ関数 Γ(x) を使います。
　Γ(n+1) = n! ですから、

画像
と定義します。これをグラフに描いてみると ......

　

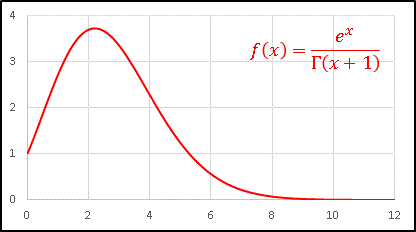
　このように滑らかな曲線が得られます。
　f(n) の各点も、もちろんこの曲線上に乗っています。
　ところで、この関数で指数部分を xcosx に変えて