画像
(3) (2) で得られた式に値を代入して、

J(2,1) = 4/3 = 1.333,　J(2,2) = J(2,3) = 16/15 = 1.067

解説23(1) の I(m, n) は ベータ関数の変数を整数に限定して少しずらしたものですから、ベータ関数の性質を反映します。 I(m, n) は m, n の増加に対して明らかな減少関数（つまり、ベータ関数は x, y の増加に対して減少関数）です。たとえば m = 2 と固定して、I(m, n) の被積分関数を

f(t) = t2 (1 − t)n
とおいて、n = 0, 1, 2 のグラフを描いてみると ......

　

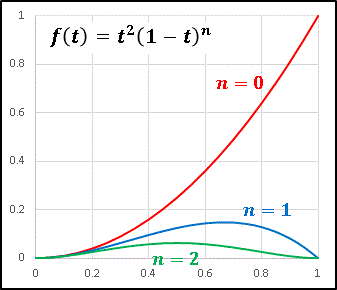
　y = f(t) の積分、すなわち y = f(t) と t 軸によって囲まれる面積が急減していく様子がわかります。 (1) の計算結果である

I(m, n) = m! n! / (m + n + 1)!
の形を見ても、分母のほうが大きく、m, n → ∞ で 0 に収束するだ