を考慮して、

nφ = iθ + 2kpi　⇔　φ = iθ/n + 2kpi/n
としなくてはなりません。結果として α = reiθ の n 乗根は

画像
と表されます。ただし周期性から k = 0, 1, 2, ...... , n − 1 です。これ以上の k を選択しても、同じ値が繰り返されるだけです。

(2) 1 の 3 乗根を求める問題です。1 = exp(0) と表せますから、(1) で得られた式に
　θ = 0, r = 1, n = 3, k = 0, 1, 2 を代入すると各 k に対応する解 xk は

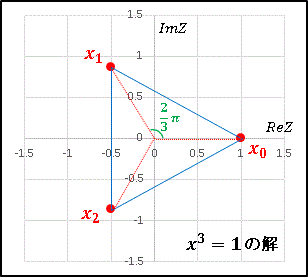
　　　x0 = exp(0) = 1
　　　x1 = exp[i(2pi/3)]
　　　x2 = exp[i(4pi/3)]

となります。次にこれらを複素平面上にプロットします。たとえば、

　　　x1 = exp[i(2pi/3)] = cos[(2pi/3)] + i sin[(2pi/3)]

ですから、 実軸に cos[(2pi/3)], 虚軸に sin[(2pi/3)] をとって対応する点を描きます。こうして各点を結ぶと正三角形が描かれます。

　

補足　複素平面　 横軸に実部（ReZ:real part）、縦軸に虚部（ImZ:imaginary part）をとり、
複素数 Z = x + iy を平面上の 2 点に対応させることができます。