与える x も同じように正方向にシフトしていきます。念のために f(x) の微分を 0 とおいて確認しておきましょう：

f'(x) = [1 - sqrt(a/x)] = 0　⇒　x = a　　（sqrt は√ のこと）
　確かに x = a で最小値 f(a) = 0 をとります。
　a = 2 のグラフを抜き出してもう少し詳しく解析していきます。

　

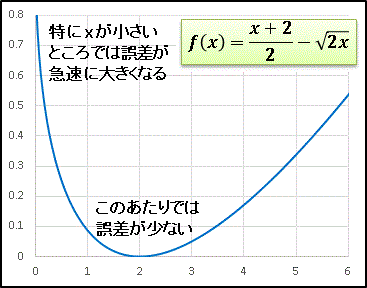
　f(x) は α と β がどのような関係のとき、「相加平均と相乗平均の差がどのくらいなのか」ということを教えてくれます。たとえば上のグラフでは、β = 2 （対称式ですから α = 2 と考えても構いません）のとき、1≦α≦3 の範囲なら誤差 0.1 未満です。α の値が β から離れていくと誤差は大きくなっていきますが、特に α が小さいほうへずれていくとき、より急速に誤差が大きくなっていくことがわかります。たとえば α = 0.1, β = 2 のとき、

　　　　相加平均 = 1.005,　相乗平均 = 0.141
　　　　[相加平均 - 相乗平均] = 0.859

となります。相加平均は２つの数値の真ん中を返す平均ですから直感的に分かりやすいのですが、相乗平均は片方の値が真ん中からずれると、（相加平均と比較して）その値を小さめに見積もる傾向があることがわかります。つまり β に対して α が小さいときには、α のほうに重心がおかれ、逆に α が大きい時には β 側に重心がおかれるということです。
　理系英単語�@　新連載のお知らせです（というほど大げさなものじゃないけど）。理工学部（特に大学院に進む