新規記事の投稿を行うことで、非表示にすることが可能です。
2023年10月25日
コラッツ予想(その5)
コラッツの数式のグラフを、実際に自分で書いてみながら、読み解いていく事にしましょう。
このグラフ内における数字の配列は、要するに、コラッツの数式に当てはめた数字がどんどん変わっていく順番を示しています。
私は、すでに、「コラッツ予想(その2)」で、「3」の数字をコラッツの数式で計算してみました。この計算の結果を、そのまま並べてみると、こんな感じになります。
3、10、5、16、8、4、2、1
これで、まずは一本の数列が完成した事になります。
お分かりのように、「3」を計算した事で、途中にある「10、5、16、8、4、2」の計算も済んでしまいました。
さて、小さな数字から片っ端から計算していくとなると、次は「6」の計算となるのですが、「6」は「3」の数列の一つ前にくっつくだけなので、特に気にする事もないでしょう。
続く「7」が、やや長めの数列となります。
7、22、11、34、17、52、26、13、40、20、10、5、16、8、4、2、1
しかし、皆さんもお気付きになったかも知れませんが、実は、この「7」の数列ですけど、「10」より下は、「3」の数列とピッタリ重なっているのであります。
だから、グラフに直しますと、「3」と「7」の数列は繋ぎ合わせる事が可能です。そうやって、結合してみせたのが、次の配列です。
7
22
11
34
17
52
26
13
40
20
10、3、6
5
16
8
4
2
1
すでに登場している数は計算済みと見なして飛ばしていき、次の新しい数字「9」は「7」の少し先、「12」も「6」の一つ前にあります。「15」も「40」のやや先の方にあるので、これも追加しちゃいましょう。
9
28
14
7
22
11
34
17
52
26
13
40、80、160、53、106、35、70、23、46、15
20
10、3、6、12
5
16
8
4
2
1
こうして、最初は一本線だったグラフも、計算が終わった数字を追加する度に、じょじょに分岐しだしました。
すでに登場している数は飛ばしながら、このまま、新しい数をどんどん付け加えていきましょう。
18
9
28
14
7
22、44、88、29、58、19、38、76、25
11、22
34
17
52
26
13
40、80、160、53、106、35、70、23、46、15
20
10、3、6、12、24
5
16、32、64、21
8
4
2
1
これで、「26」までの数字が出揃った事になりました。分岐もかなり増えてきたようです。
次の「27」は、「46」のずっと先の方に(「15」とは枝分かれして)存在しているのですが、この「27」がちょっと厄介な存在なので、ここには書き足しません。
とにかく、コラッツの数式をグラフ化すると、こんな感じで、数が増えるほど分岐していき、やがては、例の進化系統樹のような見た目へと仕上がっていくのです。
このグラフ内における数字の配列は、要するに、コラッツの数式に当てはめた数字がどんどん変わっていく順番を示しています。
私は、すでに、「コラッツ予想(その2)」で、「3」の数字をコラッツの数式で計算してみました。この計算の結果を、そのまま並べてみると、こんな感じになります。
3、10、5、16、8、4、2、1
これで、まずは一本の数列が完成した事になります。
お分かりのように、「3」を計算した事で、途中にある「10、5、16、8、4、2」の計算も済んでしまいました。
さて、小さな数字から片っ端から計算していくとなると、次は「6」の計算となるのですが、「6」は「3」の数列の一つ前にくっつくだけなので、特に気にする事もないでしょう。
続く「7」が、やや長めの数列となります。
7、22、11、34、17、52、26、13、40、20、10、5、16、8、4、2、1
しかし、皆さんもお気付きになったかも知れませんが、実は、この「7」の数列ですけど、「10」より下は、「3」の数列とピッタリ重なっているのであります。
だから、グラフに直しますと、「3」と「7」の数列は繋ぎ合わせる事が可能です。そうやって、結合してみせたのが、次の配列です。
7
22
11
34
17
52
26
13
40
20
10、3、6
5
16
8
4
2
1
すでに登場している数は計算済みと見なして飛ばしていき、次の新しい数字「9」は「7」の少し先、「12」も「6」の一つ前にあります。「15」も「40」のやや先の方にあるので、これも追加しちゃいましょう。
9
28
14
7
22
11
34
17
52
26
13
40、80、160、53、106、35、70、23、46、15
20
10、3、6、12
5
16
8
4
2
1
こうして、最初は一本線だったグラフも、計算が終わった数字を追加する度に、じょじょに分岐しだしました。
すでに登場している数は飛ばしながら、このまま、新しい数をどんどん付け加えていきましょう。
18
9
28
14
7
22、44、88、29、58、19、38、76、25
11、22
34
17
52
26
13
40、80、160、53、106、35、70、23、46、15
20
10、3、6、12、24
5
16、32、64、21
8
4
2
1
これで、「26」までの数字が出揃った事になりました。分岐もかなり増えてきたようです。
次の「27」は、「46」のずっと先の方に(「15」とは枝分かれして)存在しているのですが、この「27」がちょっと厄介な存在なので、ここには書き足しません。
とにかく、コラッツの数式をグラフ化すると、こんな感じで、数が増えるほど分岐していき、やがては、例の進化系統樹のような見た目へと仕上がっていくのです。
タグ:コラッツ予想
2023年10月22日
コラッツ予想(その4)
コラッツ予想の証明方法で、「完全に証明してみせた過程を提示する」というのは、つまりは、「全ての整数をコラッツの数式にかけてみて、1になるのを確認する」という事です。
もちろん、数(整数)は無限に存在するのですから、このような事は永遠に実現しません。コンピューターを使って、2の68乗までの数が、コラッツの数式できちんと1になる事が確認されているらしいのですが、それでもなお、コラッツ予想が証明された事にはなっていないのです。
続いて「コラッツ予想を立証する数式」ですが、こちらも、まだ誰も発見してはいないようです。コラッツ予想の解説ページを見ると、ベテランの数学者が過去に作り上げた各種の数式を見かけますが、それらはコラッツの数式の特徴を数式化したものであって、「最後が1になる事」の証明式ではないらしいです。私の無知ぶりが露呈してしまいますので、この辺に関しては、あまり深くは触れません。
本当の証明にはならないかも知れませんが、コラッツの数式における数字どうしの関連性(つながり)をグラフにしてみるという試みもあります。こちらも、コラッツ予想の解説ページを見ると、いろいろな形のグラフを目にする事ができます。
結論は一つのはずなのに、コラッツの数式の計算結果は、さまざまなバリエーションのグラフに直して、書き出せるらしいのです!
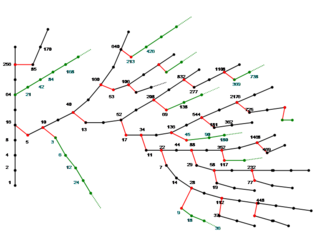
これなんかも、もっともシンプルな形のグラフの一つです。数の分岐の仕方が、まるで生物の進化系統樹のようです。過去に提示されてきたコラッツの数式のグラフは、ほとんどが、こんな形に描かれています。
大自然の摂理(進化系統樹)とソックリだなんて、なんだか、数字という概念も自然の一部である事を、あらためて実感させてくれるのです。
もちろん、数(整数)は無限に存在するのですから、このような事は永遠に実現しません。コンピューターを使って、2の68乗までの数が、コラッツの数式できちんと1になる事が確認されているらしいのですが、それでもなお、コラッツ予想が証明された事にはなっていないのです。
続いて「コラッツ予想を立証する数式」ですが、こちらも、まだ誰も発見してはいないようです。コラッツ予想の解説ページを見ると、ベテランの数学者が過去に作り上げた各種の数式を見かけますが、それらはコラッツの数式の特徴を数式化したものであって、「最後が1になる事」の証明式ではないらしいです。私の無知ぶりが露呈してしまいますので、この辺に関しては、あまり深くは触れません。
本当の証明にはならないかも知れませんが、コラッツの数式における数字どうしの関連性(つながり)をグラフにしてみるという試みもあります。こちらも、コラッツ予想の解説ページを見ると、いろいろな形のグラフを目にする事ができます。
結論は一つのはずなのに、コラッツの数式の計算結果は、さまざまなバリエーションのグラフに直して、書き出せるらしいのです!

これなんかも、もっともシンプルな形のグラフの一つです。数の分岐の仕方が、まるで生物の進化系統樹のようです。過去に提示されてきたコラッツの数式のグラフは、ほとんどが、こんな形に描かれています。
大自然の摂理(進化系統樹)とソックリだなんて、なんだか、数字という概念も自然の一部である事を、あらためて実感させてくれるのです。
タグ:コラッツ予想
2023年10月20日
コラッツ予想(その3)
コラッツの数式に当てはめていくと、なぜ、全ての正の整数が(多分)1にたどり着いてしまうのかは、数学のシロウトでも、なんとなく、その仕掛けが想像(イメージ)できるのではないかと思います。
このコラッツの数式は、要するに、「割る2」と「×3」と「+1」の組み合わせなのです。正の整数の中では、もっとも小さい、言い換えれば、自然数の基礎とも言うべき三つの数字です。よって、この三つの数字を色々と組み合わせれば、それ以上の大きな整数は、どの数字だって作り出せるのが当然のはずなのです。それは、逆も意味しています。これらの三つの数字を上手に使えば、あらゆる整数を1にまで分解してしまう事も可能な訳です。
コラッツの数式の場合は、「割る2」と「×3」の組み合わせが実に絶妙です。一見、「×3」ばかりが続けば、「割る2」が追いつかず、数は巨大化していくばかりのようにも感じられますが、ここに「偶数は2で割って、奇数は×3+1」という条件がついています。
偶数を計算したあとは偶数にも奇数にもなりますが、奇数の計算のあとは必ず偶数になってしまうカラクリなのです。つまり、確率的には、絶対に偶数の出現率の方が多くなるのであり、ゆえに、偶数の「割る2」の回数の方が奇数の「×3」の回数の方を上回る事になるのです。だから、この計算式を何度も繰り返せば、割る事の方が多くて、いずれは、最小の1にまで割れてしまうという理屈になるのです。
ここで、ひそかに重要な要素となっているのが「+1」です。この「+1」は、奇数を偶数に変える役目も果たしていますが、同時に、元の数字を1ずつ、ずらしていく効果も持っています。このように、1ずつ、ずれてゆく事によって、掛け算と割り算だけでは1には成らない数でも、少しずつ微調整された末に、やがては1にたどり着いてしまうと言う仕組みです。
コラッツの数式の構造は、言葉で説明すれば、ざっと、こんな感じなのですが、残念ながら、これだけでは、コラッツ予想を証明した事にはなりません。数学の世界には「なんとなくイメージでは」という妥協は存在せず、正解は具体的な形にしなくてはいけないからです。
つまり、以上の解説を証明したければ、それを立証した数式を構築するか、あるいは、完全に証明してみせた過程を提示しなくてはいけません。この簡単なコラッツの数式が、いまだに誰にも解明された事になっていないのは、この証明の部分が厄介だからなのです。
このコラッツの数式は、要するに、「割る2」と「×3」と「+1」の組み合わせなのです。正の整数の中では、もっとも小さい、言い換えれば、自然数の基礎とも言うべき三つの数字です。よって、この三つの数字を色々と組み合わせれば、それ以上の大きな整数は、どの数字だって作り出せるのが当然のはずなのです。それは、逆も意味しています。これらの三つの数字を上手に使えば、あらゆる整数を1にまで分解してしまう事も可能な訳です。
コラッツの数式の場合は、「割る2」と「×3」の組み合わせが実に絶妙です。一見、「×3」ばかりが続けば、「割る2」が追いつかず、数は巨大化していくばかりのようにも感じられますが、ここに「偶数は2で割って、奇数は×3+1」という条件がついています。
偶数を計算したあとは偶数にも奇数にもなりますが、奇数の計算のあとは必ず偶数になってしまうカラクリなのです。つまり、確率的には、絶対に偶数の出現率の方が多くなるのであり、ゆえに、偶数の「割る2」の回数の方が奇数の「×3」の回数の方を上回る事になるのです。だから、この計算式を何度も繰り返せば、割る事の方が多くて、いずれは、最小の1にまで割れてしまうという理屈になるのです。
ここで、ひそかに重要な要素となっているのが「+1」です。この「+1」は、奇数を偶数に変える役目も果たしていますが、同時に、元の数字を1ずつ、ずらしていく効果も持っています。このように、1ずつ、ずれてゆく事によって、掛け算と割り算だけでは1には成らない数でも、少しずつ微調整された末に、やがては1にたどり着いてしまうと言う仕組みです。
コラッツの数式の構造は、言葉で説明すれば、ざっと、こんな感じなのですが、残念ながら、これだけでは、コラッツ予想を証明した事にはなりません。数学の世界には「なんとなくイメージでは」という妥協は存在せず、正解は具体的な形にしなくてはいけないからです。
つまり、以上の解説を証明したければ、それを立証した数式を構築するか、あるいは、完全に証明してみせた過程を提示しなくてはいけません。この簡単なコラッツの数式が、いまだに誰にも解明された事になっていないのは、この証明の部分が厄介だからなのです。
タグ:コラッツ予想
2023年10月14日
コラッツ予想(その2)
さて、コラッツ予想がどんなものなのかと言いますと、wikipedia の文章をまるまる引用いたしますと、次のような数字の性質のことを指します。
ほんとは、もっと細かい数式とかも存在するようなのですが、初心者が扱うにあたっては、これだけの内容で十分です。簡単な例題をやってみましょう。
もっとも小さな分かりやすい数字で、「3」を上記の数式に当てはめてみます。
3は奇数ですから、この数式ですと「3×3+1」となり「10」という答えが導き出されます。
この10を、さらに、この数式にかけます。10は偶数ですから、2で割って、「5」に変わります。
今度は、この奇数の5を数式に当てはめて、「5×3+1」で「16」に。
偶数の16を2で割って「8」に。さらに、この偶数の8も2で割ると「4」に。この4を2で割り、「2」になったところを、もう一度、2で割ると「1」になってしまいます。
つまり、これが、この数式の性質です。同じように、どんな数字(正の整数に限る)を、この数式で計算してみても、最後は「1」になると言うのが、コラッツ予想なのです。
いかがでしょうか。
シロウトの目で見たら、そんな難しい数式の理論ではなく、当たり前の話のようにも感じられませんか。しかし、いざ、この数式の正しさを証明しようとすると、偉大な数学の博士たちでも歯が立たず、莫大な大きな数字の立証に関しては、コンピューターで計算させるしかないと言うシロモノらしいのであります。
任意の正の整数 n に対して、以下で定められる操作について考える。
n が偶数の場合、n を 2 で割る
n が奇数の場合、n に 3 をかけて 1 を足す
このとき、「どんな初期値から始めても、有限回の操作のうちに必ず 1 に到達する(そして 1→4→2→1 というループに入る)」という主張が、コラッツの予想である。
n が偶数の場合、n を 2 で割る
n が奇数の場合、n に 3 をかけて 1 を足す
このとき、「どんな初期値から始めても、有限回の操作のうちに必ず 1 に到達する(そして 1→4→2→1 というループに入る)」という主張が、コラッツの予想である。
ほんとは、もっと細かい数式とかも存在するようなのですが、初心者が扱うにあたっては、これだけの内容で十分です。簡単な例題をやってみましょう。
もっとも小さな分かりやすい数字で、「3」を上記の数式に当てはめてみます。
3は奇数ですから、この数式ですと「3×3+1」となり「10」という答えが導き出されます。
この10を、さらに、この数式にかけます。10は偶数ですから、2で割って、「5」に変わります。
今度は、この奇数の5を数式に当てはめて、「5×3+1」で「16」に。
偶数の16を2で割って「8」に。さらに、この偶数の8も2で割ると「4」に。この4を2で割り、「2」になったところを、もう一度、2で割ると「1」になってしまいます。
つまり、これが、この数式の性質です。同じように、どんな数字(正の整数に限る)を、この数式で計算してみても、最後は「1」になると言うのが、コラッツ予想なのです。
いかがでしょうか。
シロウトの目で見たら、そんな難しい数式の理論ではなく、当たり前の話のようにも感じられませんか。しかし、いざ、この数式の正しさを証明しようとすると、偉大な数学の博士たちでも歯が立たず、莫大な大きな数字の立証に関しては、コンピューターで計算させるしかないと言うシロモノらしいのであります。
タグ:コラッツ予想
2023年10月12日
コラッツ予想(その1)
NHKで「笑わない数学」という教養番組をやっているのですが、これがシロウトにも分かりやすくて、なかなか面白いです。元々は、私は、去年、「星新一の不思議な不思議な短編ドラマ」(NHK)のシリーズを通して拝見していたのですが、その時間帯の流れで放送された「笑わない数学」も、何となく観てしまい、それから、この番組にもハマってしまったのです。
で、今月になってから、その「笑わない数学」の第2シーズンが始まったのですが、昨夜は、コラッツ予想というものを紹介しておりました。
これは、簡単にいうと、一種の数字パズルみたいなものでして、実は、その仕掛けがまだ解明されておらず、数学の未解決問題の一つにも数えられていて、解決した人には賞金が出るとまで言われているのであります。
番組内でも、wikipedia を見ても、このコラッツ予想を証明する事は不可能に近いような話をしているのですが、僭越ながら、私も、このコラッツ予想の証明方法について、少し語ってみたくなりました。
とは言っても、私は、学問の数学に関しては、ズブの素人ですので、あくまで、一般人の感覚みたいな発想しか話す事はできません。もしかすると、とんだ見当違いの話を偉そうに語ってしまったり、すでに立派な数学者が解明済みの事をあらためて新発見のように再説明したりもするでしょう。
だけど、その辺は、浅はかなシロウトの未熟な意見なのだと大目に考えて、温かく見守っていただけたならば、幸いでございます。どうせ、公式な論文や討論の場でもなく、ただのどシロウトがコチャコチャッとブログにイタズラ書きした程度の内容ですので。
それでも、もし、本物の数学者や数学に詳しい専門家の方が、この駄文に目を通しておられましたら、各所のおかしな理屈とか不完全な証明などを、やさしく指摘して、修正やアドバイスでも加えていただけましたら、とても嬉しくて、助かります。
で、今月になってから、その「笑わない数学」の第2シーズンが始まったのですが、昨夜は、コラッツ予想というものを紹介しておりました。
これは、簡単にいうと、一種の数字パズルみたいなものでして、実は、その仕掛けがまだ解明されておらず、数学の未解決問題の一つにも数えられていて、解決した人には賞金が出るとまで言われているのであります。
番組内でも、wikipedia を見ても、このコラッツ予想を証明する事は不可能に近いような話をしているのですが、僭越ながら、私も、このコラッツ予想の証明方法について、少し語ってみたくなりました。
とは言っても、私は、学問の数学に関しては、ズブの素人ですので、あくまで、一般人の感覚みたいな発想しか話す事はできません。もしかすると、とんだ見当違いの話を偉そうに語ってしまったり、すでに立派な数学者が解明済みの事をあらためて新発見のように再説明したりもするでしょう。
だけど、その辺は、浅はかなシロウトの未熟な意見なのだと大目に考えて、温かく見守っていただけたならば、幸いでございます。どうせ、公式な論文や討論の場でもなく、ただのどシロウトがコチャコチャッとブログにイタズラ書きした程度の内容ですので。
それでも、もし、本物の数学者や数学に詳しい専門家の方が、この駄文に目を通しておられましたら、各所のおかしな理屈とか不完全な証明などを、やさしく指摘して、修正やアドバイスでも加えていただけましたら、とても嬉しくて、助かります。






