Excel VBA　数学実験室

　姉妹サイト『 Excel VBA 数学教室』にて数学問題掲載中！

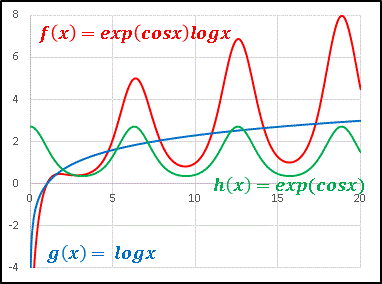
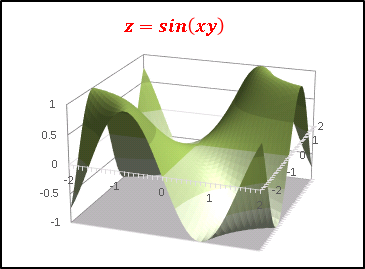
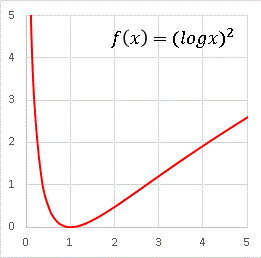
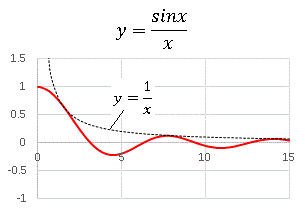
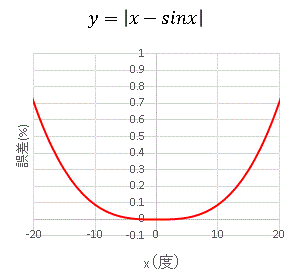
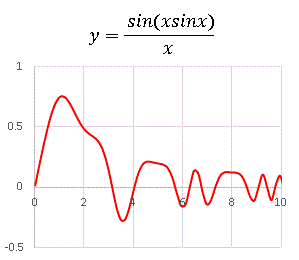
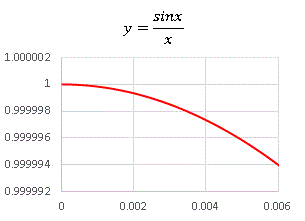グラフ全体の増加、振幅の増加、双方に寄与します

　今回扱うのは f(x) = x (a − sin²x) という周期関数です。
　a に色々な値を入れて調べてみます。

f(x) = x (1 − sin²x)

　

　a = 1 のときのグラフです。 1 − sin²x は 0 〜 1 の正の値をとるので x を乗じると 0 < x では正の範囲で振動し、 x < 0 では負の範囲で振動します。 sin²x については


という積分公式が成り立ちますが、偶関数なので区間を −π/2 まで拡張し、さらに全体を区間の長さπで割ると


という区間 [−π/2, π/2]における平均値が得られます。 sin²x は正の周期関数ですから、さらに拡張した範囲でもこの平均値は一定です。区間 [0, π] や区間 [0, 2π] でも同じです。したがって 1 − sin²x の平均値は 1/2 であることがわかり、そこに x を掛けることによって全体としては y = (1/2) x を基準とした振動関数であることがわかります。図中の緑色の細い線は y = (1/2) x を示しています。

f(x) = x (2 − sin²x)

　

　a = 2 のケース。 2 − sin²x の平均値は 1 ですから、f(x) は全体として y = x に従って増加していくことになります。 2 − sin²x に掛かる x はグラフ全体と、振幅の 2 つの増加に寄与していることになります。

f(x) = x (1/2 − sin²x)

　

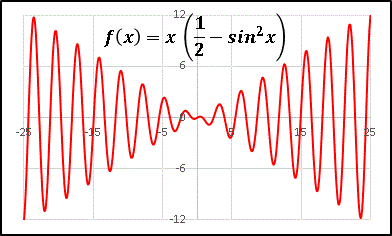
　a = 1/2 とすれば sin²x の平均値 1/2 と打ち消し合って (　　) の中の平均を 0 にします。すると x が掛かってもグラフ全体の 1 次関数的増加はありません。 x は振幅の増加のみに寄与することになります。

f(x) = x (1/2 − sin²x + cosx)

　

　最後はおまけです。 cos x を追加してみました。 cosx はもちろん周期 2 πで平均 0 の関数ですから、やはりグラフの y 軸方向へのシフトには寄与しませんが、振動の様子そのものは複雑に変えてしまいます。もはやグラフから直に判断することは難しいのですが、長さ 2 π（ cosx が加わったことにより、先ほどまでとは測るべき定規の長さが異なることに注意！）では値の平均は 0 となっているはずです。
　 　

　グラフ解析を再開します！

　数学問題のほうは、姉妹サイト『 Excel VBA 数学教室』のほうで定期掲載を続けますので、そちらもよろしくお願いします。

微分して周期の近似値を求めます

　さて今回扱うのは


という関数です。指数関数、三角関数、対数関数が揃い踏みの豪華な関数ですよ。


も一緒に Excel でグラフを描いてみましょう。

　

　h(x) は周期 2πの振幅を変えない周期関数です。そこに緩やかながらも増加関数である g(x) をかけると、振幅を増加させる周期関数 f(x) が得られます。グラフではちょっと見えにくいかもしれませんが、 h(x) と f(x) の周期はほんの僅かにずれています（特に一番左端の山の部分をよく観察してみてください）。 f(x) を微分して確認してみましょう。


　f' = 0 とおくと、 exp(cosx) > 0 ですから、


という極値を求める式が得られます。この式の解を求めるのは容易ではありませんが、x が十分に大きいところでは 1 / x は無視できますから、近似的に


とすることができて、その周期が約 2πであることがわかります。上のグラフでも、 3 つめの山になるとずれが判明できないほど周期が一致していますね。
　⇒ 円周率の表記について 　

　今回は 2 変数三角関数のグラフを載せていきます。

　最初は z = sin(x + y) という関数。

　

　直線 y = x に沿って z 軸方向に振動しています。

　次は z = sin(xy) のグラフ。

　

　四方に波打つ関数ですが、積 xy の符号によって直線 y = x に沿っては山から、y = - x に沿っては谷から始まります。

　次は sin の中身を原点からの距離にしてみます：


　変数が距離


ですから、x - y 面内の回転操作に関して対称なグラフが描かれます：

　

　これは水面に小石を落としたときの波形と同じです。

　最後は少し複雑な関数　z = xcosy + ysinx　を扱ってみます：

　

　こうなるともう色々なところに峠や窪地が現れてしまって、何が何やら分からない感じですが、眺めているだけでも楽しいものです。
　⇒ なんとなくの数学日記（Excel による等高線グラフ） 　

　ここしばらくは難しい数学が続いたので、この辺で一休みです。

拡大コピーを繰り返す波

　今回は f(x) = (logx) ² という関数をベースに変形していきます。対数関数を 2 乗しているので負の値のところは折り返すようなグラフを想像すれば大まかな形は想像できますね。エクセルでグラフを描いて確認してみましょう。



　別に微積分なんて使わなくても、logx の形さえ知っていれば、このグラフは手書きで描けます。x = 0 の点は定義されないことに注意してください。 x → 0 のときは +∞ に発散します。では次に logx の前に sinx を乗じてみます。



　全域で正の値をとる周期関数です。注目すべきは原点です。グラフではわかりにくいのですが、対数関数が含まれているので、やはり原点で値をもつことはできません。しかし x → 0 のとき、sinx → 0 の効果で、 (logx) ² の発散効果を抑え込んで関数 g(x) は 0 に収束します。つまり x → 0 の極限値はもちます。さて次に sinxlogx を 3 乗してみますと・・・・・・



　こういう不思議なグラフが現れます。このブログを頻繁に訪れてくださっている人は「あれ？　どこかで見たような？」と思われるかもしれませんね。このブログの記念すべき（？）第１回の記事では sinx の 3 乗を扱いました。再掲してみましょう。



　h(x) は sin³x の波形を拡大コピーしながら振動するような関数になっています。
　⇒ なんとなくの数学日記（サッカーとラグビーを観る予定です） 　

　微積分を習い始めた頃に教わる大切な公式の１つに、


という式がありますね。上の式は x → 0 となる極限で sinx と x が同程度の速さで 0 に収束していくことを示しています。また、上の式が成り立つからこそ、小さな x に対して


という近似式を使うことが許されているのです。

Excel で sinx / x のグラフを描いて収束を確認します

　そもそも y = sinx / x というはどのような関数なのでしょうか？　グラフを描いてみましょう。



　このグラフの形を予測することは難しくないと思います。 f(x) = 1 / x という関数に沿って振幅が減少していきます。今注目するのは原点付近の振る舞いなので、そこを拡大してみましょう。



　x, y ともに非常に小さな目盛をとっています。確かに x → 0 で y → 1 となっているようですね。ところで、 sinx ≒ x という近似式はどの程度の大きさの x で許されるのか気になったことはありませんか？　私はずいぶん昔に物理学の本で「振り子の角度が十分小さいときに sinx ≒ x と近似してよい」と書かれてあるのを見て、「え？　十分小さいとはどのぐらい？」と考えて電卓で確かめてみたことがありました。エクセルを使って改めて見てみることにします。そのために x と sinx の差を取って絶対値をとった y = | x−sinx | という関数を使って調べてみます。



　横軸は "度（degree）" の単位で、縦軸は誤差を百分率でとってあります。 x = 20°をとったとすると誤差は 0.7% 程度です。やや大きすぎる誤差かもしれません。たとえば振り子の問題で長さ L を 1m として Lsinx ≒ Lx のような計算をすると、7mm の誤差が生じてしまいます。約 1cm と考えると私としてはやはり少し躊躇しますね。 x = 10°であれば誤差は 0.1 % 未満になりますから全く問題ないでしょう。やはり x = 10°= 0.175 rad あたりまでが妥当だと思います。

　最後に少し変わった関数を作ってみたので載せておきます。 sin() の中身を xsinx とした関数です。



　かなり複雑な形をしていますね。この関数は x → 0 のとき y → 0 となります。その理由は sin() の中の xsinx が x → 0 のとき 0×0 の形になり、結果として分子のほうが分母より速く 0 へ近づいていくからです。微積分ではこういう極限の感覚を磨いていくことが大切です。