偙偽偲偺悢妛婎慴島嵗
丂嶰妏娭悢偲儀僋僩儖曇 [13]丂壛朄掕棟傪摫偒傑偟傚偆
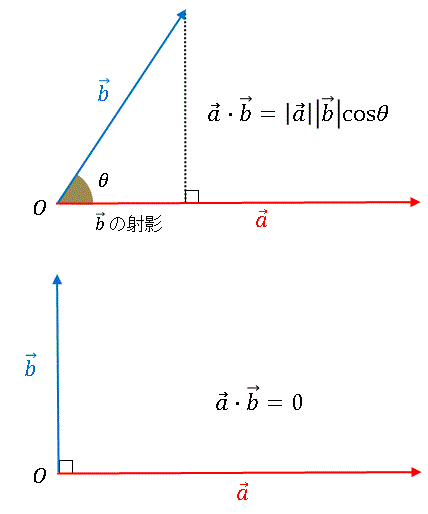
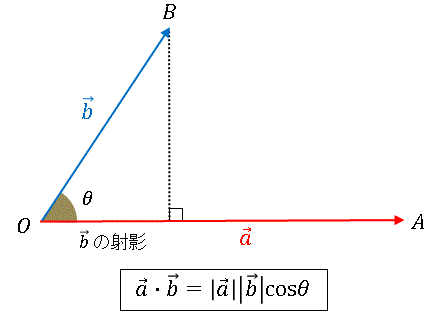
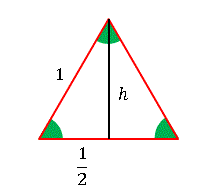
丂埲慜偺婰帠偱扨埵墌傪梡偄偰 sin30亱傗 cos45亱偺傛偆側抣傪寁嶼偟傑偟偨偗偳丄媮傔傜傟傞抣偑尷傜傟偡偓偰偄偰丄側傫偩偐怱傕偲側偄偱偡偹丅偦偙偱傕偆彮偟寁嶼斖埻傪奼戝偡傞偨傔偵 壛朄掕棟 偲偄偆岞幃傪摫偔偙偲偵偟傑偡丅偙傟傪巊偆偲 sin15亱偲偐丄tan75亱偺傛偆側抣傪媮傔傞偙偲偑偱偒傞傛偆偵側傝傑偡丅撪愊傪巊偆偲娙扨偵壛朄掕棟偑摫偒弌偝傟偰偟傑偄傑偡傛丅傑偢偼壓偺恾傪偛棗偔偩偝偄側丅丂
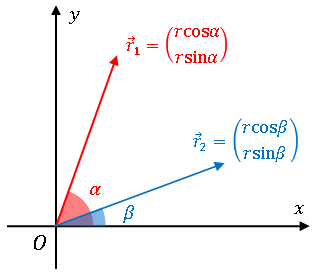
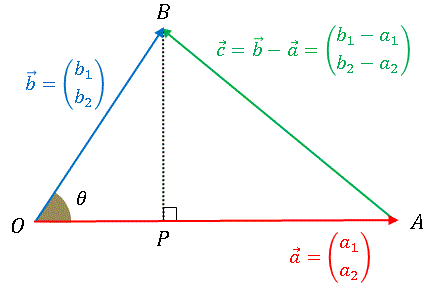
丂摨偠戝偒偝偱丄x 幉偐傜偺妏搙兛, 兝傪側偡俀偮偺儀僋僩儖
偺撪愊傪惉暘昞帵偺岞幃偱偮偔偭偰傒傞偲 ......
丂堦曽偱丄偙偺俀偮偺儀僋僩儖偺側偡妏偼 兛亅兝 偱偡偐傜丄
偲彂偔偙偲傕偱偒傞傢偗偱偡丅椉幃偼摉慠摍偟偄偼偢偱偡偐傜丄
偲側偭偰壛朄掕棟偑侾偮偱偒偁偑傝偱偡両丂巆傝偺壛朄掕棟偼偙偺幃偐傜摫偔偙偲偑偱偒傑偡傛丅傑偢忋偺幃偱 亅兝 仺 兝 偲偍偔偲丄cos(亅兝) = cos兝, sin(亅兝) = 亅sin兝 傛傝丄
偲偄偆俀偮傔偺壛朄掕棟偑摼傜傟傑偡丅師偵 (1) 幃偐傜
偲偄偆幃偑摼傜傟傑偡丅兤 = 兛 + 兝 偲偡傞偲嵍曈偼
偲側傞偺偱丄
偲偄偆岞幃偑摼傜傟傑偡丅偙偺幃偱 亅兝 仺 兝 偲偍偔偲
偲側傝傑偡丅傑偨 (2) 偲 (3) 偐傜
丂椉曈傪 cos兛sin兝 偱妱傞偲
偑摼傜傟傑偡丅偦傟偱偼嶰妏娭悢偺壛朄掕棟傪傑偲傔偰偍偒傑偟傚乣丅
丂偙傟偱崱傑偱傛傝怓乆側嶰妏娭悢偺抣偑寁嶼偱偒傞偺偹乣丅
丂嵟屻偵傂偲偮偩偗帋偟偰傒傑偟傚乣丅sin75亱偺抣傪媮傔傑偡傛丅
丂偪傖傫偲寁嶼偱偒傑偟偨偹乣丅
丂奆偝傫傕怓乆側抣偱帋偟偰傒偰偔偩偝偄側乣丅
丂偦傟偱偼傑偨師夞偍夛偄偟傑偟傚乣丅
丂 丂