≫ BlogCat の SF小説「不思議なお店営業中」Excel 3 次元グラフ(原点からの距離 r の逆数)
今回は x - y 面内における原点からの距離 r の逆数が組み込まれた関数について調べます。 r は
r = sqrt(x 2 + y 2) [1]
で定義されます。sqrt はエクセルで用いられる平方根(√)を表す記号です。Latex で全ての数式を書くのはちょっと手間がかかるので、今回から √ は sqrt で表すことにします。少しだけ楽をさせてくださいな。グラフを調べる前に、 [1] の偏微分 ∂r/∂x, ∂r/∂y を求めておきます。すでに大学で偏微分を習っている学生さんにとっては易しい演習問題ですが、まあこういう計算は繰り返しておいて損はありません。
∂r/∂x は y を定数と考えて x で微分する
∂r/∂y は x を定数と考えて y で微分する
だけのことですから、合成関数の微分を知っていれば、高校生の皆さんにとっても、さほど難しい計算ではありません。でもちょっとだけ注意点を1つ。 [1] のような式を見たとき、
r = (x 2 + y 2) 1/2
のようにみて計算してしまいがちです。「指数の 1/2 を下ろして - 1/2 にして、えーと、それから( )の中身を微分して ……」というように計算しても別に間違いではないですし、今回のような例ではさほど時間もかかりませんが、以下で説明するような計算方法を覚えておくと、もっと複雑な関数を微分するときに応用が効きます。まず [1] の両辺を2乗します:
r 2 = x 2 + y 2
それから両辺を x, y でそれぞれ微分すると、
2r(∂r/∂x) = 2x, 2r(∂r/∂y) = 2y
となって、
∂r/∂x = r / x, ∂r/∂y = r / y [2]
と簡単に求められます。距離 r の偏微分はよく出てきますから、公式だと思って覚えてしまってください。
z = 1 / r
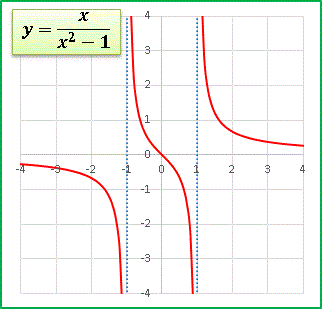
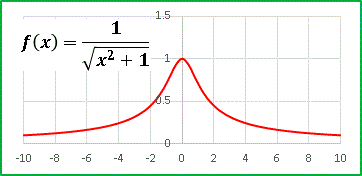
それではまず、基本となる z = 1 / r のグラフを描いてみます:
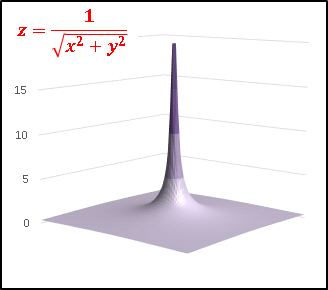
予想通りの形ですね。 r → 0 で z → + ∞ ですから、原点に聳え立つ塔は無限大の高さを持っています。もちろんコンピューターでは無限大を扱えませんから、グラフィックスで正確に描くことはできません。皆さんの想像力で補ってくださいな。さて今度は、この関数の偏微分を求めてみます。先ほど求めた r に関する偏微分 [2] を用いると簡単です:
∂z/∂x = - (1 / r
2)∂r/∂x = - x / r
3 [3]
∂z/∂y = - (1 / r
2)∂r/∂y = - y / r
3 [4]
慣れると暗算で計算できますよ。理工系の人は、こういう単純計算を面倒くさがらずに日々トレーニングです。さて [3], [4] の意味を考えてみます。 r
3 はどの点でも必ず正の値ですから、分子だけに注目します。微分の値が - x に依存しているということは、 y = c (適当な定数)という直線に沿って x を動かしたときに、
0 < x の領域では x が増加すると z が減少する
x < 0 の領域では x の増加すると z が増加する
ということです。 y についても同様のことがいえます。これは上のグラフと合わせてみると理解できると思います。要するに (x, y) が原点から離れていくと、z は減少していくということです。その傾向をもっと分かり易くみるなら、z を r の関数とみて、r で微分すればよいのです:
∂z/∂r = - 1 / r 2
この形なら r の増加にともなって z が減少していく様子がすぐに分かります。それなら別に最初から偏微分などしなくてもよさそうですが、これほど綺麗に z が r の関数で表されるのは特殊な場合に限りますから、より複雑な関数と出会ったときには、やはり偏微分を用いて関数を解析する必要があります。
z = f(x, y) = xy / r
次の例を見てみましょう。
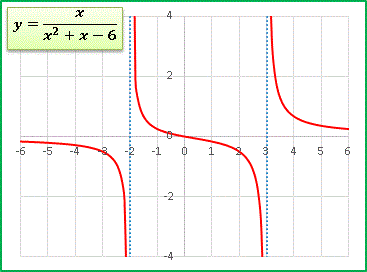
z = f(x, y) = xy / r
という関数のグラフです:
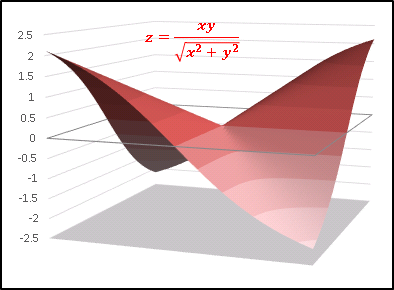
f(0, 0)は鞍点ではありません! この関数で定義されない点ですのでご注意ください。この点を中心に勾配が複雑に入り組む関数です。x, y > 0 で y = x に沿って尾根がありますね。このあたりを調べてみましょう。 x = t, y = t と置いて、z を直線 y = x の上を動く媒介変数 t の関数として表すと、
z = t / sqrt(2)
となります。つまり x, y > 0 の領域では、直線上に沿う変化に対して z は1次関数として振る舞うことがわかります。
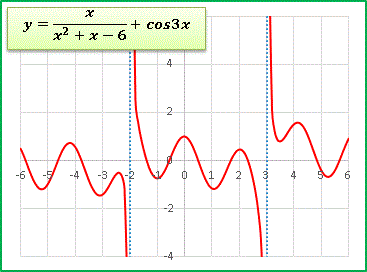
z = sinr / r
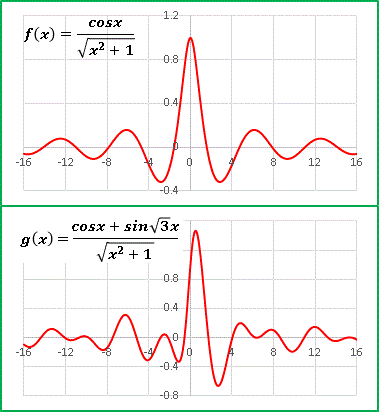
最後は三角関数と組み合わせて、z = sinr / r というグラフを描いてみます:

微積分を習い始めたときに
という定理を習いますね。以前にこのブログでも数値的に解析したことがあります。 sinx と x のどちらがより小さいのかという兼ね合いで極限値 1 が定まります。1変数のときは x 軸に沿って原点に近づけました。 z = sinr / r では x - y 面内のどの方向から原点へ近づいても極限 1 をとるという意味になります。だから中心に高さ 1 の突端が生じるのです。
⇒ なんとなくの数学日記(コーヒーに砂糖は入れません)






![03[1+sinπx]平方根.gif](/excelmathfunction/file/035B12BsinCF80x5DE5B9B3E696B9E6A0B9.gif)
![04[2次関数/2次関数]平方根①.gif](/excelmathfunction/file/045BEFBC92E6ACA1E996A2E695B0EFBC8FEFBC92E6ACA1E996A2E695B05DE5B9B3E696B9E6A0B9E291A0.gif)
![05[2次関数/2次関数]平方根②.gif](/excelmathfunction/file/055BEFBC92E6ACA1E996A2E695B0EFBC8FEFBC92E6ACA1E996A2E695B05DE5B9B3E696B9E6A0B9E291A1.gif)