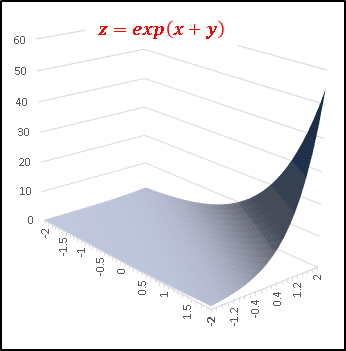
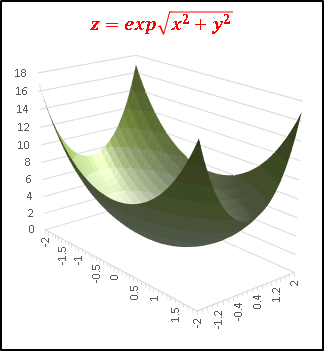
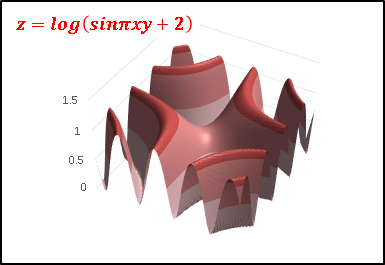
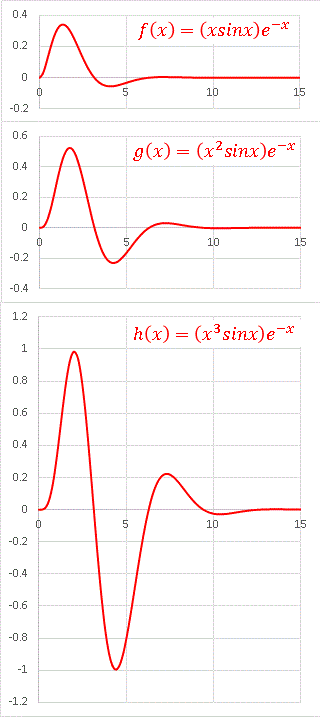
�ɒl�̗L���̋��ڂ肵�܂�
�@����͈ꌩ�����Ƃ���ƂĂ��Ղ�������y = exp(x) �| ax 2�@�@�@[1]
�Ƃ������������܂��B a �̒l���������I��ŃO���t��`���Ă݂܂��B
�@
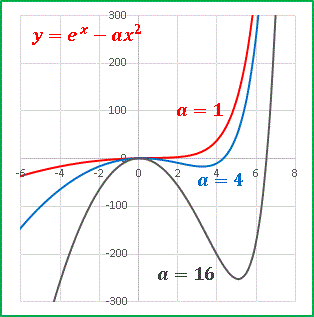
�@a �̒l��傫������قǐ[���J���`������ exp(x) �̑�����x�点�܂��B���͂��̊��� a �̕ϑJ�ߒ��ł��鏊�����Ɂu�ɒl�������Ȃ����v����u�ɒl�������v�ւƕω����܂��B���̗l�q�ׂ邽�߂ɁA[1] ��������ē����܂��F
y�� = exp(x) �| 2ax�@�@�@[2]
�@���̓����̃O���t���`���Ă݂܂��B
�@
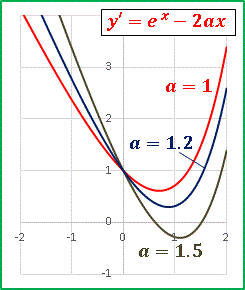
�@y�� �̃O���t�� x ���ƌ�_�����Ă� [2] �͋ɒl�������܂��B
�@a = 1.2 �ł͂܂��ɒl�͂���܂��Aa = 1.5 �͋ɒl����ł��B
�@������ a �̒l��ω������āu�ǂ��� x ���Ɛڂ��邩�v�Ƃ������Ƃׂ܂��B����� VBA �Ńv���O�����������Čv�Z������킯�ł����A�ȒP�ɂ��̍\�����������Ɓu a �̒l�� 0.001 ���݂ɕω������āAy�� �̒l���P�ł����̒l���Ƃ����u�ԂɌv�Z���~�߂āA���̂Ƃ��� a ��臒l�Ƃ݂Ȃ��v�Ƃ������̂ł��B���m�Ɍ����A�u�v�Z���~�߂� a �v�ƁA�u���̒��O�� a �v�Ƃ̊Ԃ�臒l������܂��B���ݕ��������������萸�x�̍����l�邱�Ƃ��ł��܂��B���ۂɂ��̃v���O���������s����ƁA���̂悤�Ȍ��ʂ܂��B
�@a = 1.360 �Ōv�Z�I��
�@�@x = 0.96�@y = 0.000496
�@�@x = 0.97�@y = - 0.000456
�@
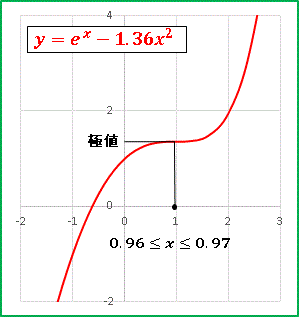
�@a = 1.360 ��臒l�ł��B���̒l���ߎ��I�ɃO���t�� x ���ɐڂ��� a �ł���ƍl����ƁA���̂Ƃ� y��= 0 �̉� x = xm �͂ЂƂ����ł���A x = xm �̑O��� y���̕����͕ω����܂���B���������ċɒl�͂����܂���B���������ɍl����� a = 1.360 �ŋ͂��� x ���ƌ������Ă���̂� y�� = 0 �̉��͂Q����A���̉� �� �� �� �i�� < ���j�͔��ɋ߂��l���Ƃ�܂��B�����Ă��̑O��� y�� ���܂������ɕω����āAx = �� �̂Ƃ���ŏ�ɓʁi�ɑ�l�j�Ax = �� �̂Ƃ���ʼn��ɓʁi�ɏ��l�j������܂��B���������͈͂ɋɑ�l�Ƌɏ��l���o�����Ă���̂ł��B���͂ł��炸�珑���Ă������������킩��Ȃ��Ȃ肻���Ȃ̂ŁAa = 1.370 �Ƃ����O���t�ŋɒl�t�߂�͈͂��g�債�Ă݂܂��F
�@
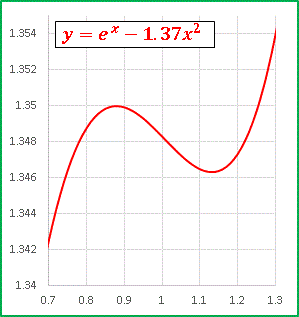
�@�����Ɖ��ʂ�����Ă��܂��B
x = �� = 0.88 �̂Ƃ��ɑ�l 1.350
x = �� = 1.14 �̂Ƃ��ɏ��l 1.346
x = �� = 1.14 �̂Ƃ��ɏ��l 1.346
�ƂȂ�܂��B�ɑ�E�ɏ��Ƃ����Ă����ʂ̃O���t�ł͖ڂɌ����Ȃ����x�̏����ȋN���ł��B
�@�� �Ȃ�ƂȂ��̐��w���L�i�V�����u���O���n�߂܂����j �@