Excel で確率的に変化する数列を作ります
漸化式
f(1) = 1, f(n + 1) = f(n) + 1
で表される数列はただの等差数列です。
横軸 n に対して縦軸 f(n) をプロットすると各点は直線の上に乗ります。
そんなグラフを描いても仕方ないので、次のような数列を考えてみます:
f(1) = 1, f(n + 1) = f(n) + R
ここで R は次のように定義されます:
R = + 1 (50%), −1 (50%)
つまり「前項に半々の確率で 1 を加えるか引いて次項を作る」という数列です。n = 1 から n = 50 まで計算させてプロットします。これを1つの試行とします。この数列は確率的に振る舞うために、試行のたびに異なる形のグラフが描かれます。それでは3回試行してグラフを描いてみます。
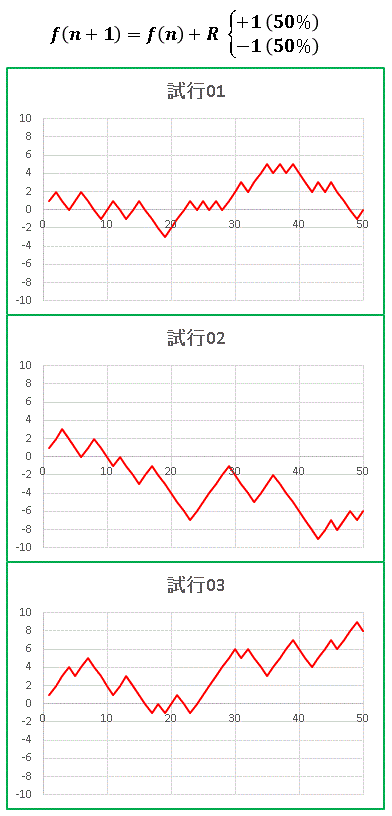
3つのグラフは全て異なる振る舞いをしていますね。試行 01 では f(n) は 0 のあたりをうろうろしています。試行 02 では f(50) は負の方向に大きくふれていて、試行 02 では f(50) は + 8 まで達しています。+ 1 も −1 も半々の確率ですから、感覚的には試行 01 のように 0 付近に留まっていそうな気がしますが、個々の試行では必ずしもそうならないようです。
次は 10 回の試行を繰り返してその平均をとってみます。つまり、試行 01 の各項を f1(n), 試行 02 の各項を f2(n) …… としたときに平均項を
fav(n) = [f1(n) + f1(n) + ・・・・・・f10(n)] / 10
と定義してグラフをプロットすると次のようになります:

平均をとると各項がほぼ 0 になっていることが分かります。これは直感と一致しますね。しかし「グラフが全体的に少しプラス側に寄っているような …… 」と気づいた人は鋭いです。私も「平均をとるための試行回数が少ないかな?」と考えて試行回数を増やして何度も確認しましたが、やはり少しだけプラス側にふれるという結果を得ました。
おそらくこれは確率 50 % を計算するために使用している乱数( VBA の Rnd )に問題があるようです。Excel の RAND() や VBA の Rnd はあまり精度のよくない疑似乱数(線形合同法)を用いています。したがって今回のような計算をすると、どうしてもその精度の低さが目に見える形で現れてしまい、「うーむ」と頭を抱えてしまうことになるのです。私は乱数生成については詳しくないので、問題を解決するにはどこからかアルゴリズムを持ってくるしかありません(さすがに1から勉強してプログラムを書くのはしんどいです)。最近ネットで調べたところ、メルセンヌ素数を利用する「メルセンヌ・ツイスタ」というアルゴリズムが優秀で Excel にも実装可能らしいので、1度試してみようかなと思っています。
⇒ なんとなくの数学日記(私の好きな漫画ベスト3(修正版))