Excel VBA　数学実験室

≫ [Amazon書籍] これだけはおさえたい理工系の基礎数学（Primary大学テキスト）

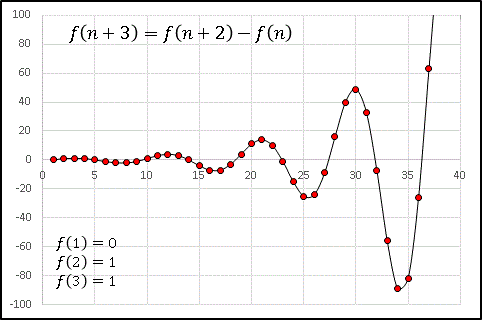
絶対値を含んだ３項間漸化式

　絶対値を含んだ３項間漸化式


をプロットすると、とても面白いグラフになります。

　

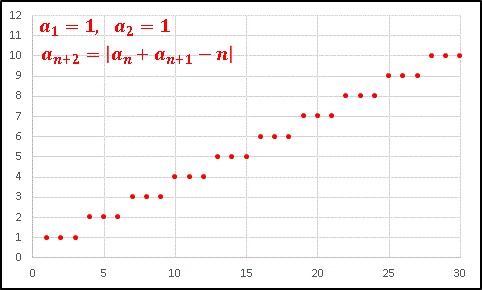
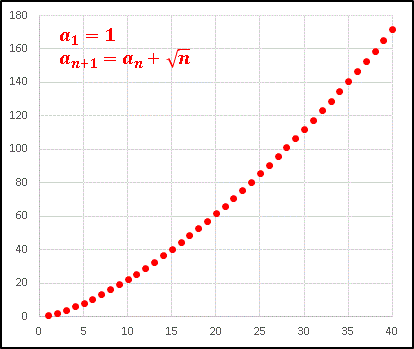
　連続する３つの項が同じ値をとって、次に１つだけ値を増す、ということがずっと繰り返されています。階段のような数列ですね。

予測できない数列（局地的に不規則です）

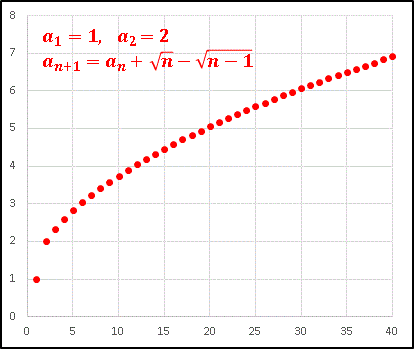
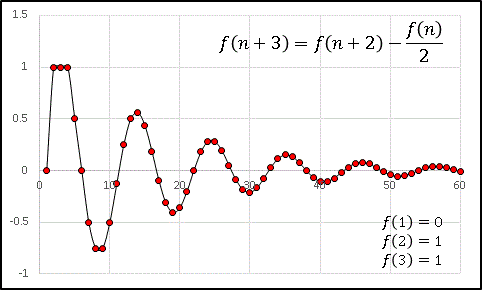
　次は少しだけ漸化式の形を変えて


としてみると様相を一変させます。

　

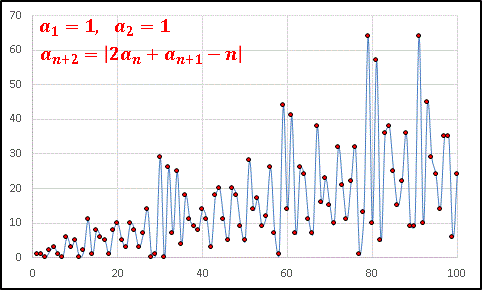
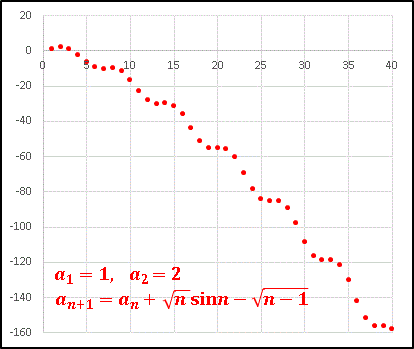
　見やすいように点を線で結んでいます。
　規則があるんだかないんだか、よく分かりませんね。
　a_n は上がったり下がったりしながらも、全体としては少しずつ大きくなっていくようです。もう少し先まで様子を見てみましょう。

　

　n = 400 までプロットしています。
　幅が狭いので、点を省いて平滑線だけで描いています。
　やはり局地的には不規則なのですが、全体としては振れ幅を増加させていますね。いずれにしても、何だか乱雑な数列に思えますが、この数列は初期値に応じてその姿を全く変えてしまいます。たとえば a₂ = 3 としてみると ......

　

　とても整然とした数列が現れましたね。
　規則的に上がって下がってを繰り返しながら、直線的に値を伸ばしています。

波束のようなかたまりが並んでいます

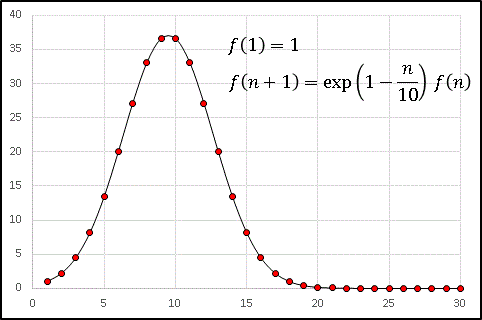
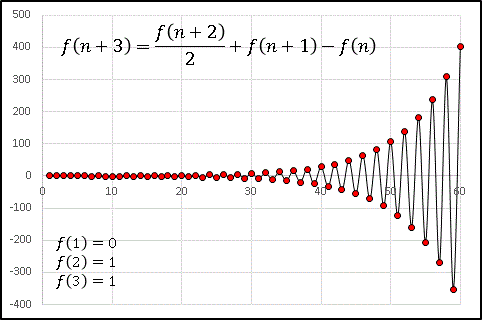
　最後にまた漸化式の形を少し変えて


として、点をプロットしてみると ......

　

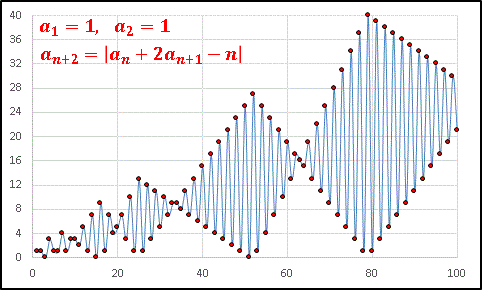
　波束のようなかたまりが並んでいます。不思議ですねえ。この数列も初期値に応じて目まぐるしく姿を変えるので、皆さんもぜひエクセルで試してみてください。
　 　

≫ [Amazon書籍] あたらしい情報数学

階差 √n の数列

　次のように階差 √n で定義される数列を考えます。


　一見して簡単そうに見えますが、Σ√n を簡単に表すことができないので、階差数列の公式を使っても一般項を求めることができません。というわけでエクセルに頼りましょう。

　

　n が小さいうちは緩やかなカーブの上に乗っていますが、n が大きくなってくるとほぼ直線的に並びます。次は


という数列です。各項に加えられる数字はかなり小さくなります。



　ほぼ予想通り n が大きくなるほど値の増加率が落ちてゆく数列ですね。
　次は三角関数を組込んで、


という数列をプロットしてみましょう。

　

　...... かなり変わったグラフになりましたね。エクセルではこうした複雑な漸化式も簡単に扱えるので。皆さんも色々試して面白いものが見つかったらぜひ教えてください。
　 　

　初項 1, 公比 3 の等比数列

　　1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, ...

の各項を 5 で割ったときの余りを並べてみると、

　　1, 3, 4, 2, 1, 3, 4, 2, ...

というように周期 4 で同じ数字が繰り返されます。このように、ある種の単調な規則をもつ数列は、各項を適当な数で割って余りを並べてみると周期性があることがわかります。

平方数の剰余数列

　平方数を並べた数列

　　1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, ...

を 3 で割って余りを並べてみると

　　1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, ...

というように周期 3 で (1, 1, 0) を繰り返します。 4 で割ってみると

　　1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, ...

というように 1 と 0 を繰り返すだけです。平方数を 4 で割った余りは 1 か 0 であることは一般的によく知られた事実です。

立方数の剰余数列

　立方数を並べた数列

　　1, 8, 27, 64, 125, 216, 343, 512, 729, ...

の各項を 2 で割って余りを並べてみると

　　1, 0, 1, 0, 1, 0, 1, 0, ...

となっています。立方数は奇数と偶数が交互に現れるということです。

a_n+1 = 3a_n + n

　漸化式 a_n+1 = 3a_n + n で定義される数列

　　1, 4, 11, 26, 57, 120, 247, 502, 1013, 2036, ...

を 4 で割って余りを並べてみましょう。

　　1, 0, 3, 2, 1, 0, 3, 2, 1, 0, 3, 2, ...

　これは周期 4 の数列となっていますね。

フィボナッチ数列

　前の２項を足して次の項を作るという、有名なフィボナッチ数列

　　1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

もまた剰余に関して周期性があります。たとえば 11 で割って余りを並べると

　　1, 1, 2, 3, 5, 8, 2, 10, 1, 0, 1, 1, 2, 3, 5, 8, 2, 10, 1, 0, ...

というように周期 10 の循環数列となります。剰余はエクセルの MOD関数を使えば簡単に調べられるので、皆さんも色々な数列で試してみてください。
　 　

≫ [Amazon書籍] 信号処理入門（図解メカトロニクス入門シリーズ）

指数関数を組込んだ数列

　f(1) = 1 として


という数列を考えてみます。具体的に並べてみると

　　　f(1) = 1
　　　f(2) = exp(8/10) f(1) = exp(8/10)
　　　f(3) = exp(7/10) f(2) = exp(15/10)
　　　f(4) = exp(6/10) f(3) = exp(21/10)
　　　・・・・・・・・・・・・・・・・・

という具合になります。横軸に n, 縦軸に f(n) をプロットして滑らかな曲線でつないでみましょう。

　

　このように１つの山を作ります。n = 0 〜 18 までは n = 9, 10 のピークを中心に左右対称になっています。 n = 19 以降は f(n) → 0 に収束します。

三角関数を組込んだ数列

　次は f(1) = 1 として


という数列です。エクセルでグラフを描いてみると ......

　

　段丘のような図になっています。 n = 1 から減衰して、いったん平らになったあとまた減衰して最後は 0 に収束します。
　 　

≫ 姉妹サイトで算数の難問に挑戦！「小太郎君のテストの点数」

振動数列になるような漸化式

　f(1) = 0, f(2) = 1, f(3) = 1 として３項間の漸化式


によって定義される数列を考えます。具体的に書くと

　　　f(4) = f(3) − f(1) = 1
　　　f(5) = f(4) − f(2) = 0
　　　f(6) = f(5) − f(3) = −1
　　　・・・・・・・・・

のようになります。さて、この数列を横軸に n, 縦軸に f(n) をとって図示すると面白い形が現れます。

　

　数列の各点を滑らかな線で結ぶと、f(n) は次第に振幅を増加させる振動関数のようになっているのです。漸化式の形が少しでも変わるとグラフの様子は一変します。今度は


という数列を図示してみましょう。

　

　今度は振幅自体がとても小さくなったうえに、減衰振動関数となりました。さらに


で定義される数列のグラフを描いてみると ......

　

　正負の符号が交互に反転するグラフとなりました。
　皆さんも何か面白い数列を見つけたらコメントください。