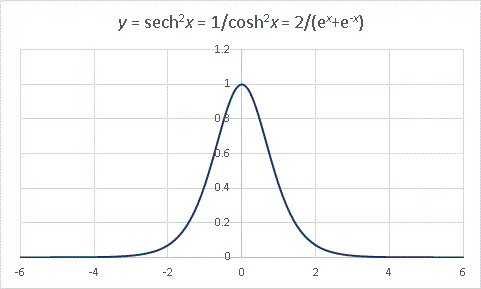
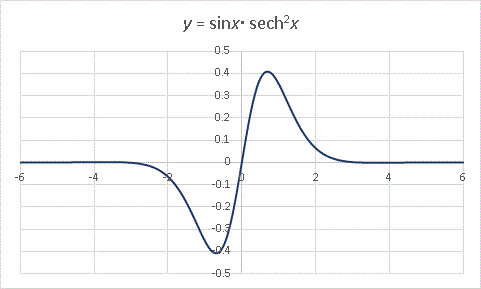
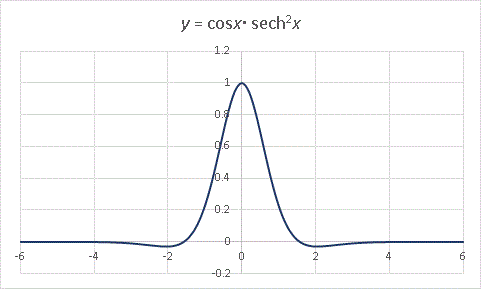
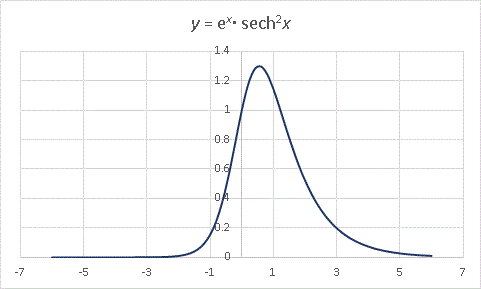
���������g���ĊK�i�O���t�����܂�
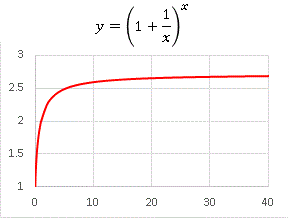
�@����͏����ς�������̍������Љ�܂��B�܂��ŏ��ɁA�@�@�@f(x) = x + cosx
�@�Ƃ��������G�N�Z���ŕ`���Ă݂܂��B
�@
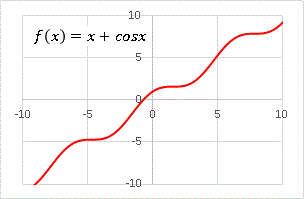
�@����͗\�z�ʂ�̌`�ł��ˁB���� y = x �ɉ����悤�Ȏ������ł��B����ł͂��̊�������� f(x) �̒��ɓ��ꂽ�ʑ����l���܂��B�܂�A
�@�@�@g(x) = f [f(x)]
�@�@�@�@�@ = f [x + cosx]
�@�@�@�@�@ = (x + cosx) + cos(x + cosx)
�@�Ƃ�������q�ɂȂ��������l����킯�ł��B�O���t��`���ƁE�E�E�E�E�E
�@
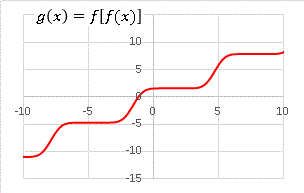
�@�i�u�̂悤�ȃO���t���o�����܂����B����ɁA
�@�@�@h(x) = f[g(x)]�@
�@�Ƃ�����������Ă݂܂��傤�F
�@
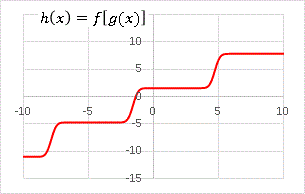
�@�S�̓I�Ɋp�����`�ɂȂ�܂����ˁB�Ō�ɂ����P�x�A
�@�@�@i(x) = f[h(x)]
�@�Ƃ����悤�ɕϊ�����ƁE�E�E�E�E�E
�@
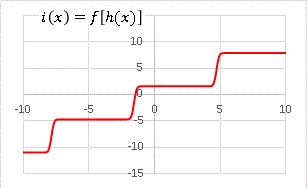
�@�K�i�̊����ł��B i(x) �̋�̓I�ȕ\���͑����ɕ��G�ɂȂ��Ă���͂��ł��B��v�Z�ō������������͎̂���̋Ƃł��傤�B������ Excel ���g���Ə�̂悤�ȕϊ��� 1 �N���b�N�Ŏ��s�ł��܂��B��̓I�Ȏ��̌`���킩��Ȃ��Ă��O���t��`�����Ƃ��ł���̂ł��B���ɂȂ����ς��Ă݂�ƁA�F�X�Ɩʔ��������o�����܂��B���������������ŗV��ł݂܂��傤�B
�@�@�@f(x) = x + cosx + sin2x
�@�Ƃ����`�ŕϊ����`���܂��B������ x �ɑ� f �ɂ���� 1 ��̕ϊ����قǂ��������� F1 �A2 ��ϊ��������� F2 �Ə����Ɩ��Ă����܂��F
�@�@�@F 1 = f(x)
�@�@�@F 2 = f [F1]
�@�@�@F 3 = f [F2]
�ł� F3 �̃O���t���G�N�Z���ŕ`���Ă݂܂��B
�@
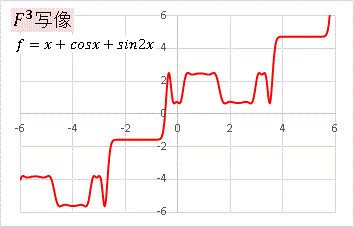
�@�n�`�̂悤�ȃO���t������܂����ˁB���G�Ȋ��ł����Ă��O�p���ƂP�����̑g�����Ȃ̂ŁA�ڂ��Â炵�Ă݂�ƁA������Ǝ��������邱�Ƃ��킩��܂��B���ɂȂ�����A
�@�@�@g(x) = x + cosx + sin2x + 1
�Ƃ����悤�ɏ����ς��āAg �ɂ���� 3 ��ϊ����� G3 �ʑ��̃O���t��`���Ă݂�ƁE�E�E�E�E�E
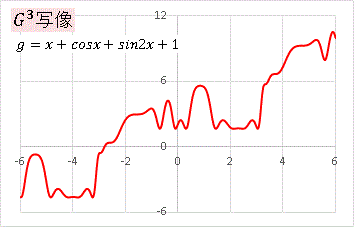
�@�n�`�̌`���ς��܂����ˁB
�@�@�� �Ȃ�ƂȂ��̐��w���L�i�i�r�X�R�J�b�v�������ς܂����j �@