Excel VBA　数学実験室

【Excelショートカット豆知識】
　[Shift] + [Space]　行を選択する
　[Ctrl] + [Space]　列を選択する

�@ルジャンドル多項式　Legendre polynomial

　ルジャンドル微分方程式


　の解がルジャンドル多項式であり、 [−1, 1] の範囲で


と表されます。ルジャンドル多項式は次の漸化式を満たします：

　　　　(2n + 1)xP_n(x) = (n + 1)P_{n + 1}(x) − nP_{n - 1}(x)

　具体的には次のような形になります：

　　　　P₀(x) = 1
　　　　P₁(x) = x
　　　　P₂(x) = (3x² − 1) / 2
　　　　P₃(x) = (5x³ − 3x) / 2
　　　　・・・・・・・・・

�AExcel でルジャンドル多項式のグラフを描きます

　Excel でグラフを描いてみると・・・・・・

　

　この図からわかるように、一般に

　　　　P_n(1) = 1

を満たします。P₀(x) において n を大きくしてゆくと、[−1, 1] の区間にたくさんの波が閉じ込められている様子がよくわかります。たとえば P₅₀(x) のグラフを描いてみると・・・・・・

　

　このように区間を限定して 各項の係数をうまく調整すれば、その内部ではあたかも cosx や sinx のように振る舞う疑似的な周期関数を作ることができます。仮にルジャンドル多項式の定義域を拡大したとしても、[−1, 1] を超えた場所に波は存在しないので、単調増加あるいは単調減少となり、そのような関数はほとんど用途がありません。任意の関数を展開するためにも波形の存在する区間に限っておく必要があります。別記事にある正規化されたエルミート多項式 u(x) は [−∞, ∞] で定義されていましたが、非常に収束の早い関数ですから、グラフを見ても実質上は −4 〜 4 のあたりに存在する波であると考えることができます。

�Bルジャンドル多項式の直交性

　ルジャンドル多項式の直交性は、


によって表されます。また [−1, 1] で値をもつ任意の関数はその範囲内で


というように展開でき、その係数 c_n は


で与えられます。

ルジャンドル多項式の応用

　変数 x を cosx 或いは sinx に置き換えると、−1 ≦ cosx, sinx ≦ 1 ですから、実数全域で定義される使いやすい関数となります。P_n(cosx) のグラフを描いてみると：

　

　小さな波と大きな波が交互に現れる関数です。電磁気学で多重極展開（電荷の作る電位を求める表式）と呼ばれる手法にはこの形が用いられます。
⇒ ルジャンドル多項式を計算する Function マクロ（ユーザー定義関数） 　

【Excelショートカット豆知識】
　[Ctrl] + [PageDown]　次のシートに移動する
　[Ctrl] + [PageUp]　　前のシートに移動する

�@ エルミート多項式　Hermite polynomial

　エルミート多項式 は次のような形で表される多項式です：


　[n/2] はガウス記号で n/2 を超えない整数であることを表しています。エルミート多項式は次のような漸化式を満たします：

　　　　H_{n + 1}(x) = 2xH_n(x) − 2nH_{n − 1}(x)

　具体的に書き表すと、

　　　　H₀(x) = 1
　　　　H₁(x) = 2x
　　　　H₂(x) = 4x² − 2
　　　　H₃(x) = 8x³ − 12x
　　　　・・・・・・・・・

のような形になります。グラフに描くと下のような形になります：

　

�A エルミート多項式の正規直交化

　エルミート多項式 H_n(x) を正規直交化すると次のような関数になります：


　u_n(x) は−∞ < x < ∞ の範囲で直交する関数です：

　
　δ_mn は m = n のときだけ値 1 をもつという記号（クロネッカーのデルタ）です。 u_n(x) のグラフを描くと次のようになります：

　

　u_n(x) は量子力学における１次元調和振動子の固有関数として知られています。古典力学の振り子に相当する現象ですが、量子の世界では n によって振動の状態が決定されます。 n の値はエネルギー E_n を定めます。 n が大きいほど E_n が大きく、激しく波打つ関数になります。最もエネルギーの低い u₀(x) は振動しているというよりは、x = 0 近辺にとどまっているという状態ですね。

　u₁(x) で変数 x を x³ に変えてみると・・・・・・

　

　ピークの幅が狭くなりますが、極大値・極小値は変わりません。同じように変数 xⁿ において n を大きくしていけば、ピークはどんどん鋭くなっていきますが、極値そのものが変化するわけではありません。

　u_n(x) は線形微分方程式の解なので、u_m(x), u_n(x) を適当に選んで重ね合わせてもやはり微分方程式の解となっています。例として u₂(x), u₅(x) を足し合わせてみます：

　

　複雑な関数に見えますが、要は axⁿ + ・・・・・・という形の多項式に exp(−x²/2)を掛けただけの比較的単純な関数です。
　⇒ エルミート多項式を計算する Functionプロシージャ 　

　数ある直交多項式の中でも、第１種チェビシェフ多項式は扱いやすい関数です：


　n は整数です。負の値でも構いませんが定義から


が成り立ちます。 arccosx は逆三角関数です。逆三角関数に馴染みのない人のために簡単に説明しておくと、


という関係があります。高校数学で「 cosθ = a となるようなθ」のような書き方をすることがあると思いますが、それを逆三角関数を使って


のように表すわけです。 a には cosθ のとりうる範囲しか指定できないはずですから、逆三角関数の定義域は [−1,1] と極めて限定された範囲となります。また、


です。第１種チェビシェフ多項式は cosx の倍角公式そのものです。たとえば n = 2 のとき、


のように展開することができます。cos(arccosx) = x ですから、


というように２次関数となります。チェビシェフ多項式は


という漸化式を満たすので、T₀(x), T₁(x) から順番に次の関数を得ていくほうが簡単です。

T₀(x) から T₃(x)グラフに描いてみます：

　

　T₀(x), T₁(x), T₂(x), T₃(x) はそれぞれ直線、１次関数、２次関数、３次関数となっていますね。ただし、定義域が [−1, 1] の非常に狭い範囲に限定されていることに注意してください。

　実はチェビシェフ多項式の集合 {T_n(x)} はそれ自身が直交系をなすわけではありませんが、 T_n(x) を 1 − x² の 4 乗根で割った関数が互いに直交し、さらに pi / 2 で割ると正規直交系を作り出します。つまり次のような式が成り立っています。

第１種チェビシェフ多項式の応用

　T_n(x) を用いて合成関数を作るときは、x の中に入れる関数 f(x) の値域（すなわち T_n(x) の定義域）に [−1, 1] という制限がかかります。たとえば f(x) = exp(x) のような形で T₁(x) の中に放り込んでしまうと、exp(1) = 2.718 などの値が生じて T₁(2.718) はたちまちエラーを返します（arccos2.718 が計算不能なことに起因します）。
　そうした場合は exp(x) の値域が [−1, 1] の中に入るように改めて x の定義域を決め直さなければなりません。もちろん面白いグラフを探そうと思うなら、そういう手間を惜しんではなりません。ちょっと試みてみましょう。 f(x) = exp(x) は f > 0 の単調増加関数ですから、新しい定義域は exp(x) → 0 となる x → −∞ から、exp(x) = 1 となる x = 0 まで、すなわち (−∞, 1] となります（左側は開区間）。
　T₃(expx), T₅(expx), T₇(expx) をまとめて描いてみます：

　

　すべて x → −∞ で 0 に、 x → 0 で 1 に収束します。番号 n が増えるほど波の数が多くなりますが、波は原点付近で圧縮されていきます。

第１種チェビシェフ多項式の拡大定義

　チェビシェフ多項式は n が整数で定義されていますが、 n を実数 ν（ニューと読みます） に拡大することは簡単です：


　ただし、この場合はもはや多項式の形に書くことはできなくなります。漸化式もありません。グラフを解析するには上の式を使うしかないので手計算は大変ですが、 Excel を使えば別にどうということもありません。ν = 1 から 2.2 まで少しずつ変化させたグラフを載せてみます：

　

直線が少しずつたわむようにして２次関数へと変化し、そこからまた左上の先端が曲げられて３次関数へと変化していく様子が見てとれます。このような性質は n を実数へ拡大してみて初めてわかります。

　チェビシェフ多項式は変数 x を x^k （ k は正整数）という形に変えても、定義域 [−1, 1] をそのまま使えます。拡大定義された関数で ν = 2.5, 3.5, 4.5, 5.5 のグラフを描くとこうなります：

　

　グラフは大きく２つのタイプに分けられますね。

　　ν = 2m + 1 / 2 のときは　T_ν(0) = −pi / 2
　　ν = 2m + 3 / 2 のときは　T_ν(0) = pi / 2

というように、原点でとりうる値が２種類あります。

第 2 種チェビシェフ多項式

　第 2 種チェビシェフ多項式は次のように定義されます。


　x = cosθ とおけば、


という形で表されます。U_n(x) は 漸化式


を満たすので、 U₀, U₁ がわかれば n = 3 以降は簡単に表式を求めることができます：

　　　U₀(x) = 1
　　　U₁(x) = 2x
　　　U₂(x) = 4x² − 1
　　　U₃(x) = 8x³ − 4x
　　　・・・・・・・・・

　それでは Excel のグラフで描いてみます：


　第 1 種チェビシェフ多項式とよく似た関数系ですね。しかし、第 1 種チェビシェフ多項式が −1 ≦ x, T_n(x) ≦ 1 を満たしていたのに対して、第 2 種チェビシェフ多項式の場合は x に関しては −1 ≦ x ≦ 1 ですが、U_n(x) の値に関しては制限がありません。 n が大きくなると狭い定義域の中で非常に大きな値域をとるようになります。たとえば n = 11 としてみると・・・・・・



　両端で U₁₁(±) = 12 という値をとります。両端の値と番号 n の間には、


という関係があります。ちなみに端点は最初の三角関数を用いた定義式では分母が 0 になるので、 x → ±1 の極限値で定義されることに注意してください。多項式の形では普通に ±1 の値を代入すれば簡単です。

　U_n(x) は T_n(x) と次のような形で関連づけられています。


　つまり、 T_n(x) の任意の点における傾きが n・U_n−1(x) で与えられるわけです。 T_n(x) が３次関数であれば、その導関数は２次関数ですから、n は１つずれる形になっています。

第 2 種チェビシェフ多項式の応用

　第 1 種のときと同じように、n を実数に拡大定義してみます：


そして n = 0 から �冢 = 0.2 刻みで n = 1 まで変化させてみます：


　変遷過程のグラフ（ n = 0.2, 0.4, 0.6, 0.8 ）は直線 y = U₁(x) を左端で大きく折り曲げたような形になっています。全て x → −1 で −∞ に発散する関数です。
　⇒ 第 1 種チェビシェフ多項式を計算する Functionマクロ 　

【Excelショートカット豆知識】
　[Ctrl] + [+]　セルの挿入　　[Ctrl] + [-]　セルの削除

[1]sin(mx)cos(nx) の積分

　有名な積分公式の１つに


というものがありますね。m, n は任意の整数です。
(m, n) = (1, 1) の場合の被積分関数を図示してみます：



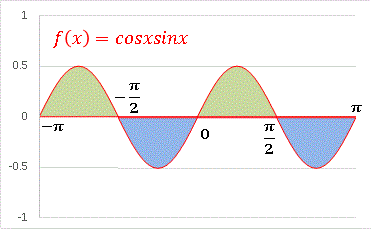
　図から明らかなように、上の公式の意味は、−pi < x < pi の範囲において、緑色の部分（正の面積）と青色の部分（負の面積）が同じことを意味しています。 (m, n) = (1, 2), (2, 1), (1, 3) の場合もまとめて見てみましょう。



　(m, n) が大きくなるほど関数の形は複雑になりますが、どのような場合でも緑の面積と青の面積は必ず相殺します。これを cosx と sinx が（あたかもベクトルのように）「直交している」と表現します。実は関数というのは、無限次元空間のベクトルなのです。関数の積分はベクトルの内積に対応しています：

　積分して 0（関数が直交）　⇔　内積が 0（ベクトルが直交）

　一般化した議論は少し難しいのですが、このブログでは具体的で目に見えるかたちで「正規直交関数系」を説明していきます。数学�Vの「積分」を習得していれば、やさしい内容だと思います。

[2]sin(mx)sin(nx) の積分

という積分公式を扱います。積分値を pi で割っていることに注意してください。m ≠ n の場合から見ていきましょう。 (m, n) = (1, 2), (2, 3) とした場合の被積分関数を描いてみます：

　

　積分値が 0 なので今のところ必要はないのですが、今後の記述との統一性も考えて、被積分関数を


　というように √pi で割った正弦関数の積と考えてください。[−pi, pi] の範囲で積分が 0 になるということ、言い換えると sinx / √pi と sin2x / √pi が直交するということは、緑の面積と青の面積が等しく、相殺するということです。「関数が直交する」という表現には、なかなか感覚が馴染めないかもしれませんが、今のところはこのグラフのイメージとセットで頭の片隅に置いておいてください。次回以降にもう少しだけ詳しくお話します。
　次は m = n の場合、つまり積分が値を持ち、２つの関数が直交しない場合です。 (m, n) = (1, 1), (2, 2), (3, 3) のときの被積分関数を並べます：

　

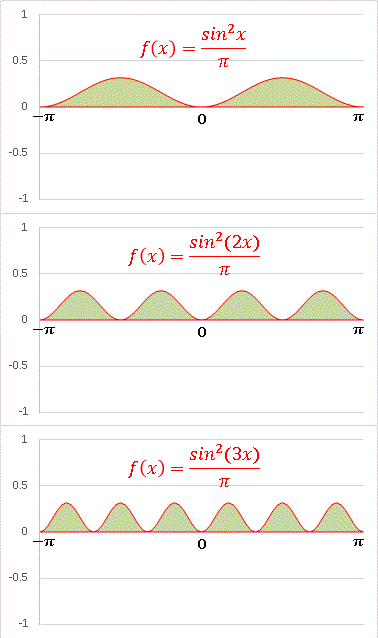
　正弦関数を 2 乗しているので、全領域で f(x) ≧ 0 です。公式は「 m, n の選び方に関わらず必ず積分値が 1 となりますよ」と言っているのですから、この３つ並んだグラフの緑色の面積は全て等しいということになります。m = n = 1 であったときの二つの大きな山が、(m, n) が大きくなるにつれて、どんどん小さな山に分裂していきます。 m = n = 11 の場合を見てみましょう。

　

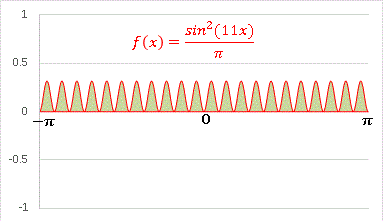
　とても小さな山（というより丘かな？）がずらずらと並んでいますね。これらを全て足し合わせて面積は 1 となります。

[3]cos(mx)cos(nx) の積分

という公式をグラフで確認してみます。δ_mn は、m = n のときだけ値 1 をもち、それ以外は 0 という記号です。m = n = 0 の場合は、被積分関数が定数 1 ですから、特に意味はありません。積分計算して公式通りに値が 2 になることを確認しておいてください。 m = n = 1 の場合を見てみます：



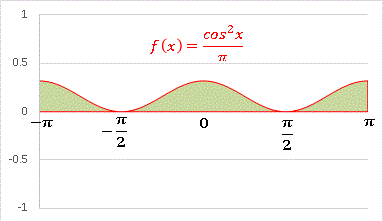
　当たり前ですが、同じ関数同士の積は決して直交しません。ベクトルでいうところの「互いに平行である」という状態です。緑の部分を全部足すと面積が 1 となります。

　次に (m, n) = (1, 2) の場合を描いてみると・・・・・・



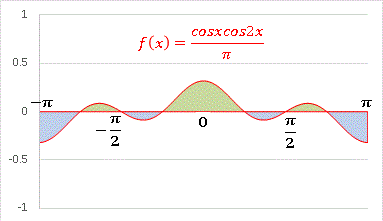
　緑と青の面積は相殺されて 0 となります。つまり cosx / √pi と cos2x / √pi は「互いに直交して」います。

三角関数の正規直交系

　これまでに扱った３つの公式をまとめると：

　
　cos 同士の積で m = n = 0 のときは被積分関数が定数となるので、１つだけ φ = c（定数）という形の関数が混ざりますが、c・cosx も c・sinx も [-pi,pi] で積分すると 0 になるので、c と cosx, c と sinx は直交しています。上の公式を見ながら次のような集合をつくってみます：


　集合内の適当な関数を２つとってみて、互いに直交していることを確認してください。
　この集合が「直交関数系」であるということになります。

　集合内のそれぞれの関数の 2 乗を積分した値が 1 になることも確かめてみてください。
　この条件が満たされていれば、集合は「正規直交関数系」であるといえます。

　それにしても、正規直交関数系を作るのは結構手間がかかりますね。わざわざこんな面倒なことをするのは、「任意の関数を直交関数形で展開する」という実用的な理由の他に「自然界の性質を記述する微分方程式の解そのものが直交系をなしている」ことが多いからです。たとえば、量子力学で水素原子の振る舞いを記述するためにラゲール多項式という直交関数系が必要となります。「なぜ必要なの？」と問われても、「自然界がそうなっているから」としか答えようがありません・・・・・・。このあたりのことは、いずれサイドバーに別のコーナーを設けて、もう少し深いところまでお話したいと思います。

　２つの関数が「直交しているかどうか」ということを積分して確認するのは結構重労働ですが、Excel を使うと、あたりをつけることができます。たとえば上の公式では (m, n) は整数に限っていましたが、 (m, n) = (1/2, 1/2) として、cos(x/2) と sin(x/2) は直交しているでしょうか？ Excel でさくっと確かめてみましょう。

　

　正負の面積は相殺されています。明らかに直交していますね。

　正規直交関数系をつくることができるのは三角関数だけに限りません。
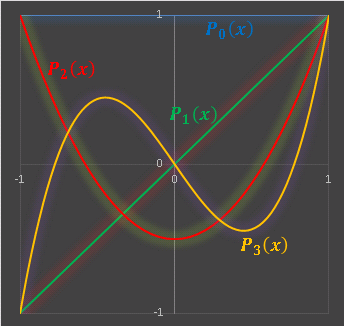
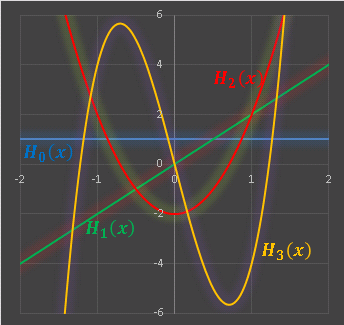
　実はごく普通の n 次関数から工夫して正規直交関数系をつくりだすことができます。三角関数に比べると議論の細部はかなり難しいので省きますが、次回からは「これらの関数は直交していますよ」という前提で、いくつかの直交多項式のグラフを紹介していく予定です。初回は比較的簡単なチェビシェフ多項式を扱う予定です。

　余力のある人は下の一般論も読んでおいてください。

【付録】正規直交関数系の一般論
　関数 y = f(x) を区間 [a,b] で、


というように xn 個の点で表すことにします。 n が有限であっても、次のようにある程度関数の形を予測することはできますね。



　つまり、関数を「 n 次元ベクトル形式で表示した」ということになります。
　ここで n → ∞ とすると、f(x) に関する完全な情報が得られるはずです。
　２つの n 次元ベクトル a, b の内積：


に対応する形で、関数 f と g の内積を


のように積分の形で定義します。 f 同士の内積は


となり、その平方根 |f| はベクトルでいうところの大きさに相当し、関数が区間 [a, b] でどれぐらいの大きさかという目安になります。a・b = 0 のとき、ベクトル a, bは直交しますが、それに対応して


のとき、関数 f(x) と g(x) は直交すると定義します。ここで、


というように n 個の関数の集合を考えます。集合内の全ての関数について


となるように適当な定数で割って規格化しておきます。

そして集合内から任意で選んだ２つの関数について、


が成り立つならば、集合｛φ_k｝が正規直交関数系であると定義します。
　⇒ なんとなくの数学日記（ポテトサラダとウスターソース）