�@����͉��߂�
���^�ϊ��i�P���ϊ��j�̈Ӗ� ���l���Ă݂悤�Ǝv���܂��B�����n�̊w������͍s��̌v�Z������������K�����Ǝv���܂����A�s��͂����v�Z�K�����߂����̂ł͂���܂���B�����ɂ͂����ƈӖ�������܂��B
���^�ϊ��i���Ƃ͐V�������W�n�̒P�ʊi�q�x�N�g���ł��j
�@���Ƃ��Ύ��̂悤�ȑΊp�����̓������s��ɂ��ϊ����l���Ă݂܂��傤�B
�@����������ό`�����
�@�̂悤�Ȍ`�ɂł��܂��ˁB�x�N�g��
a = (3, 1) ��
b = (1, 3) �ɂ����^�����̌`�ɂȂ��Ă��܂��B (x, y) �͔C�ӂ̓_�ł�����A�u x-y���W��̂�����_��
a ��
b �̐��^�����̏�ɏ��܂���v�Ƃ������Ƃł��B�܂� (X, Y) ��
a ��
b �ɂ���č����i�q�ŕ\�����V�������W�Ƃ������ƂɂȂ�܂��B�C�ӂ̓_�ł͂킩��ɂ�����������܂���̂ŁA(1, 1) �� (2, 2) �������ɕϊ����Ă݂܂��F
�@�����}������Ɖ��̂悤�ɂȂ�܂��B
�@�@
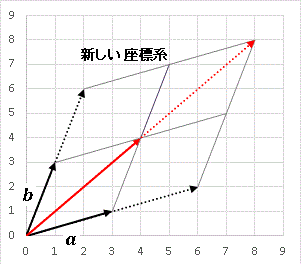
�@(1, 1), (2, 2) �͂��ꂼ�� x-y ���W�n�ł� (4, 4), (8, 8) �Ɉڂ��Ă���킯�ł����AX-Y ���W�ł͂�͂� (1, 1), (2, 2) �ƕ\����܂��B�������A���̊i�q�P�ʂ�
a ��
b �̒����ɂȂ��Ă���̂ł��B���̂悤�ɉ��߂���ƁA 2 �s 2 ��̍s��� 2 �����x�N�g�����Q���ɕ��ׂ����̂ƍl���邱�Ƃ��ł��܂��B�����Ă��̂Q�̃x�N�g�������Ƃ�т܂��i�܂�
�V�������W�n�̒P�ʊi�q�x�N�g�� �ł��j�B
�@�ȏ�̂��Ƃ܂���ƁA�s��v�Z�ɂ�����x�K�n������i����͂ƂĂ���Ȃ��ƂŖ��ӎ��ɂł���悤�ɂȂ�Ȃ��Ƃ����܂���j�A�����ʓ|��������܂��A�s����x�N�g���ɕ������A���ۂɎ��Ƀx�N�g���ō�����i�q�������Ă݂āA�u�ǂ������ӂ��ɕϊ����ꂽ�̂��ȁH�v�Ɗm�F���邱�Ƃ��J��Ԃ��Ă݂Ă��������B�K���ȍs���I��łP�O�炢����Ă݂�ƁA���^�ϊ��̖{�����K���u�����āv���܂��B
�@����܂ʼn��x����舵���Ă�����]�s��ɂ����^�ϊ����u���^�����v�̎��_�Ō������Ă݂܂��B��]�s�� R
�� �ɂ��ϊ������̂悤�ɏ����\���܂��F
�@�x�N�g��
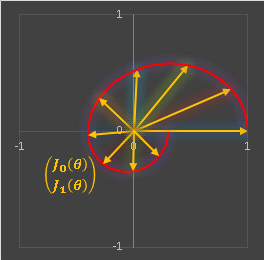
a = (cos��, sin��) �͉~����̓_�ł��ˁB
cos(�� + 90��) = - sin��
sin(�� + 90��) = cos��
�ł�����A�x�N�g��
b = (- sin��, cos��) ����͂�~����̓_�ŁA
a ���v���� 90����]�������x�N�g���ł��B
a ��
b �̓��ς��Ƃ��Ă݂�ƁA
�ƂȂ蒼�����Ă��邱�Ƃ��킩��܂��B�܂��A
|a| = 1,�@|b| = 1
�������Ɍv�Z�ł��܂��B�܂�A��]�s�� R
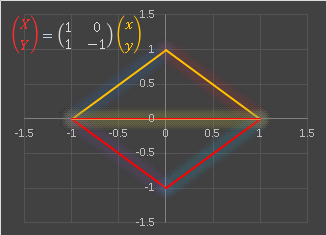
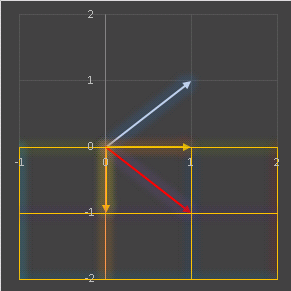
�� �͍��W���v���ɉ�]�����A�i�q�̒����Ɗp�x�͕s�ςɕۂ��܂��B���Ƃ��Ή�]�s��ŒP�ʃx�N�g�� (1, 1) ��ϊ�����Ɖ��}�̂悤�ɂȂ�܂��F
�@
![��]�s����W�ϊ�.png](/excelmathfunction/file/E59B9EE8BBA2E8A18CE58897E5BAA7E6A899E5A489E68F9B.png)
�@���F�̒P�ʃx�N�g��
e �͕ϊ��ɂ����
a +
b �ƕ\����܂�����i�ԐF�x�N�g���j�A��]�����������W�� (1, 1) �ƕ\����܂��B�������悤�ł����A�x�N�g�� (j, k) ����^�ϊ������Ƃ��A���� x-y ���W�n�ł͂��̍��W��ς��Ă��܂��܂����A�V�������W�ł͂��̂܂� (j, k) �ƂȂ�܂��B
�@
�� �Ȃ�ƂȂ��̐��w���L�i�T�C�g���f�U�C�����Ă݂����ł��j
�@


![��]�s����W�ϊ�.png](/excelmathfunction/file/E59B9EE8BBA2E8A18CE58897E5BAA7E6A899E5A489E68F9B.png)