Excel VBA　数学実験室

≫ 姉妹サイト「Excel VBA 数学教室」もよろしくです！

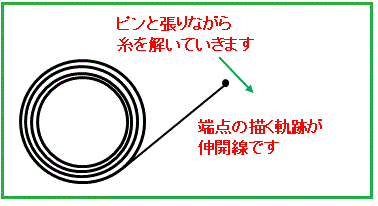
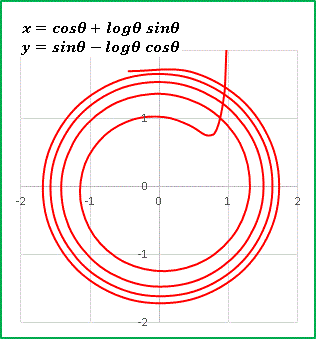
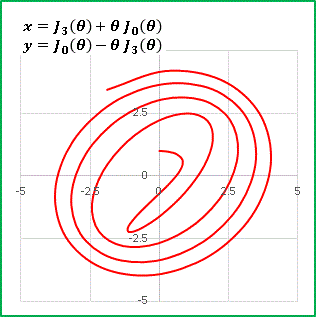
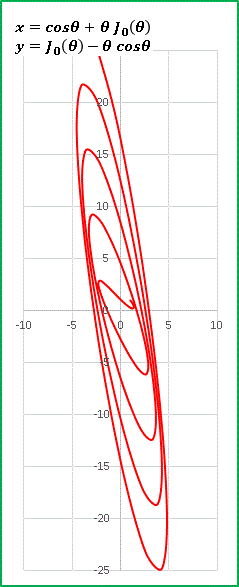
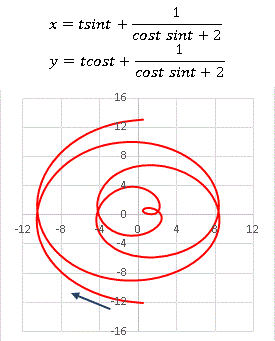
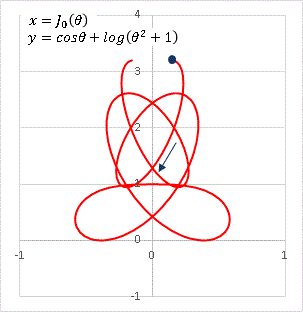パスカルの蝸牛形（リマソン曲線）

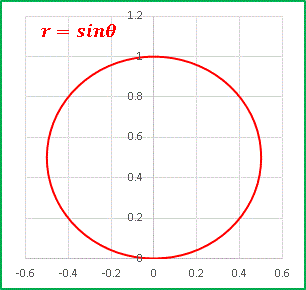
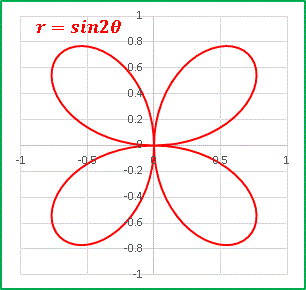
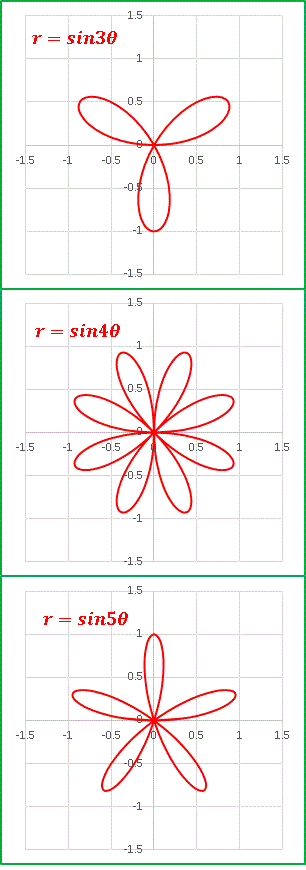
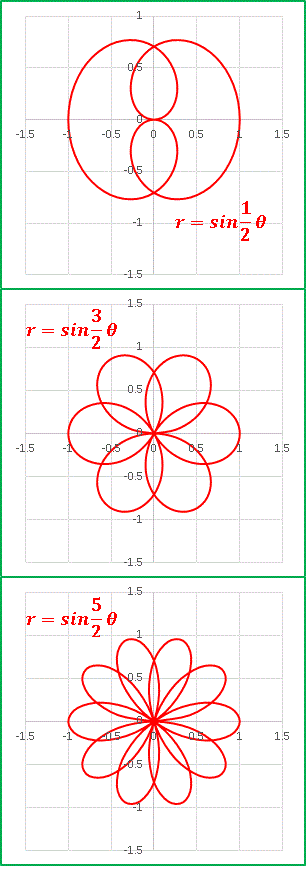
　今回は パスカルの蝸牛形 を見ていきます。読んで字のごとく「カタツムリに似た形」ということです。別名の リマソン もラテン語で「カタツムリ」という意味です。正直言うと別にそれほどカタツムリに似ているわけではありません。まあそれはともかくとして極方程式は


です。(x, y) の具体的な表式は


となります。まず a = l = 1 のグラフを調べてみます。

　

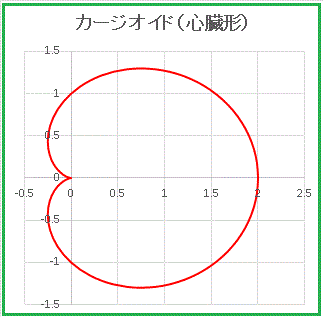
　心臓のような形をしていますね。 a = l のグラフには、カージオイド（心臓形）という名前がついています。英語で綴ると cardioid ですが、一般に英語で「心臓」を意味する heart とは無縁の響きですね。カージオイドはギリシア語の καρδιά（心臓）と είδος (形）という言葉に由来しています。カージオイドはエピサイクロイドという関数（来年早々に扱う予定です）の特別な形としても現れてきます。それではこのカージオイドからスタートして、パラメータの a, l を変化させてみましょう。まずは l を 1 に固定して a = 2, 3, 4 としてみます：

　

　カージオイドのときに凹んでいた部分を巻き込んで内側に閉曲線を作っています。 a の値が増えるほど内側の曲線は大きくなっていきますね。 a = 100 という極端な設定でグラフを描いてみると・・・・・・

　

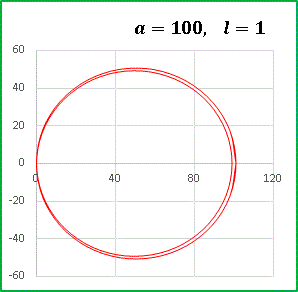
　このように、外側の曲線と内側の曲線は今にも重なって１つの円になりそうです。実際、[1] - [3] 式において a が l に対して十分に大きい（a ≫ l ）として l を落としてしまえば、

　　　　　r = acosθ
　　　　　x = acos²θ
　　　　　y = acosθsinθ

という形になりますが、これを x と y の式に書き直してみると


という円の方程式になることがわかります。つまり、[1] において a → ∞ の極限をとれば、それは１つの円となることを意味しています。

　次は a = 1 に固定して l = 2, 3, 4 と変化させてみます：

　

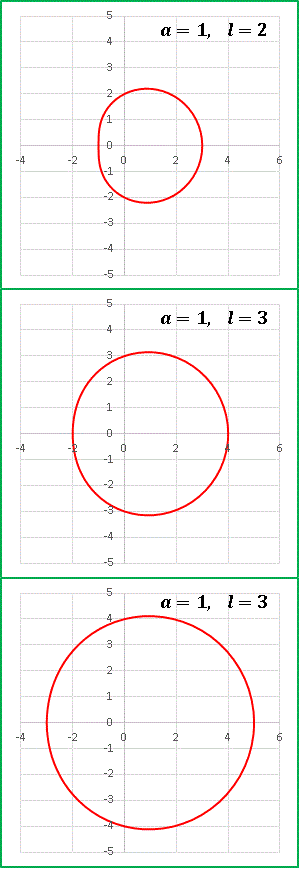
今度はより単純な１つの閉曲線が描かれていますね。 l が大きくなるほど左側の歪みが直されて真円に近づいています。今度は [1] - [3] 式で l ≫ a と考えて a の含まれた項を無視してしまうと、


という誰もが知る円の極方程式となります。 [1] において l → ∞ の極限をとってもやはり円になるということです。

　[2] [3] 式に手を加えて


という関数を考えてみます。三角関数の位相を定める p と q が加わって、


という 4 つのパラメーターでグラフの形を決定することになります。来年扱う予定のハイポサイクロイドやエピサイクロイド（或いはそれらを包括するトロコイド）に形が似ていますが、符号が若干異なっているので混乱しないでください。グラフは全く別物です。試しに (a, l , p, q) = (1, 2, 2, 1) でグラフを描いてみましょう。

　

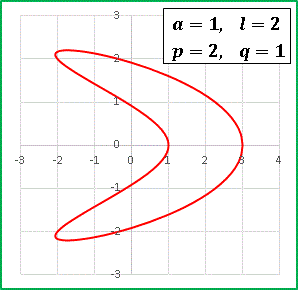
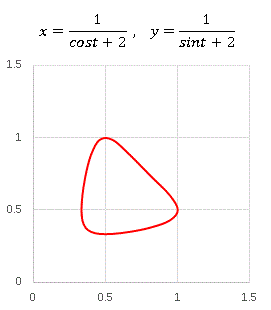
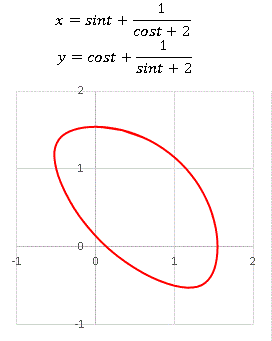
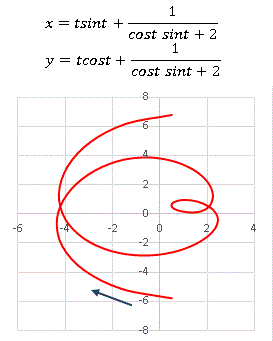
　ブーメランのような形ですね。或いは柿の種？　まあ名前はついていないので好きなように呼んでください。[4][5] はパラメータを変えると目まぐるしくその様相を変えます。私があれこれ試して面白いと思ったグラフを下に並べておきます。



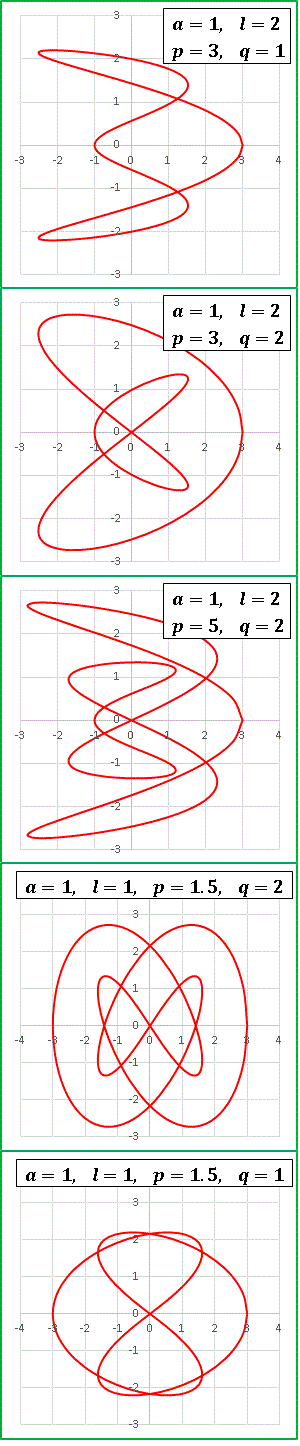
　他にも無数のパターンがあるので、エクセルをいじるのが好きな人は色々と試してみてください。何か発見があったらコメントで教えていただけると嬉しいです。
　⇒ なんとなくの数学日記（こばとの数学基礎講座再開のお知らせ） 　

【Excelショートカット豆知識】
　[Shift] + ↑　選択セルを追加しながら上に移動
　[Shift] + ↓　選択セルを追加しながら下に移動
　[Shift] + →　選択セルを追加しながら右に移動
　[Shift] + ←　選択セルを追加しながら左に移動

円の伸開線（インボリュート）

　今回扱うのは　円の伸開線（インボリュート）です。円に巻かれた糸をピンと張りながら解いていくときにできる糸の端点が描く軌跡です。

　

　(x, y) は θ を介して次の方程式を満たします。


　a = 1 としてグラフを描いてみます：

　

　原点付近から始まって間隔一定の螺旋を描いていますね。伸開線の方程式を次のように変形してみます。


ただし 0 < θ としておきます。 a = 1 のグラフは・・・・・・

　

　無限遠方からやってきて、(1, 1) 付近をかすめて屈曲します。そのあとは伸開線と同じように螺旋を描き始めますが、間隔は一定ではなく少しずつ狭まっていきます。これはもちろん logθ の影響です。θ が大きくなるほど θ の増加を抑えようとする効果が大きくなるわけです。

　伸開線の方程式において、次のように三角関数をベッセル関数に置き換えてみます：

方程式は


となります。

　

　少し傾いた楕円になってはいますが、伸開線とよく似ていますね。最後は sinθ の部分だけを　J₀(θ) で置き換えた方程式です：

　縦軸・横軸のスケールを揃えたグラフを載せてみましょう：

　
　y 軸方向に細長い楕円型螺旋が現れました。
　⇒ なんとなくの数学日記（こばとの数学基礎講座冬休み編） 　

　極座標において原点からの動径（距離） r と偏角 θ によって


の形に表された方程式を極方程式とよびます。上式から (x, y) 座標は、


で計算されます。

正葉曲線（バラ曲線）

　今回は正葉曲線


を扱います。これまでもサイクロイドやアステロイドなどを紹介ましたが、正葉曲線は動径と偏角の間の関係式がより簡単な形をしています。しかし、その方程式の描く図形はサイクロイド・アステロイドよりも複雑な形をしています。まず n が 1 の場合から見てみましょう：

　

　これは中心点が (0, 1/2) で半径 1/2 の円です。 n = 2 としてみると・・・・・・

　

　４つの葉が現れましたね。 n = 3, 4, 5 とまとめて見ていきましょう：

　

　n によって葉の数が増えますが、n が増加するに応じて葉が増えるという単純な関係にはなっていないようです。 n = 5 では葉が５枚に減ってしまっていますね。しかし n と葉の数は倍数関係にあるようです：


　グラフは省略しますが、同様に n を増やしていくと、葉数は 1n, 2n の数を交互にとることがわかります。増えたり減ったりです。さて、 n = (2m + 1) / 2 とした場合はより複雑な図形を描くことになります。 n = 0.5, 1.5, 2.5 をまとめて見てみます：

　

　複雑ではありますが、見事な対称性をもった美しいグラフです。もう少し踏み込んでいきましょう。 n = 0.3 および n = 1.3 はどうなるか・・・・・・

　

　もはや葉の形はしていませんね。細かな網目模様が出来上がっています。n が整数の場合とどうしてこんなに違ってしまうのか？　それは三角関数のもつ周期に原因があります。たとえば、


という方程式において出発点（ θ = 0 ）では


ですね。原点にいます。θを動かしてぐるりと１周してきた場合に


とやはり同じ値に戻ることがわかります。以降は繰り返しです。つまり θ をどれだけ動かしても、同じところをなぞることになります。ところが、


という方程式の場合、θ = 0 に 2 pi を加えると（１周させると）、


となり、１周前と別の値をとってしまいます。

　

ここからさらに θ を増加させていくと、１周前とは別の道筋を通ることになり、こうして周回ごとに少しずつずれた軌跡を描き続けて網目模様を作り出すわけです。y = sin(nx) というグラフはどのような n を選んだとしても、波形の山と山、谷と谷の間隔が異なるだけですが、動径 r と関連付けられた場合は「１周ごとの平面上の位置のずれ」として現れてきます。
　正葉曲線は θ の係数に対して sensitive に反応してその様相を変えます。いうなれば、係数と三角関数の周期の相性によってその形を決めます。

正葉曲線の分析

　正葉曲線がどうしてこのような特徴的なグラフを描くのでしょう？


の方程式をもう少しだけ詳しく調べてみます。動径 r は偏角 θ と sin 関数と結びついているわけですから、動径が周期的に伸縮するというのは直感的にわかります。�刄ﾆ = 15°の散布図で様子を見てみましょう。下に添えてある図は y = sin2x のグラフです。

　

　sin2x は 0 から 45°まで増加する関数ですから、そこまでは螺旋関数のように動径が伸びていきます。しかし 45°を超えると今度は一転して動径を縮ませていき、θ = 90°で長さを 0 にします（原点に戻ります）。ですから第１象限では直線 y = x に関して対称な「葉のような形」のグラフを描くわけです。
　⇒ なんとなくの数学日記（天麩羅蕎麦と鴨南蛮） 　

　ベッセル関数と他の関数を組み合わせて媒介変数表示関数を作ると、色々と面白いグラフが出現します。まずはベッセル関数と対数関数を組み合わせてみましょう。

　　x(θ) = J ₀(θ),　y(θ) = log(θ ² + 1)

という関数です。θの範囲を -4pi < θ < 4pi としてグラフを描いてみると・・・・・・



　青い点がスタート地点の (x(-4pi), y(-4pi))です。上の方からジグザグに x 軸まで降りて来て、またジグザクに舞い上がっていきます。

複雑でありながら調和のとれた美しい形のグラフを描きます

　次はこれを少し変形して y(θ) に cosθを加えてみましょう。



　とても複雑な軌道を描く関数です。複雑ではありますが、調和のとれた綺麗な形のグラフです。媒介変数表示関数は基本的に y = f(x) のような簡単な形に表せないので、描画前にグラフの形を予測することは不可能なのです。「この関数はどんな形のグラフを描くのかな？」とわくわくしながらエクセルを操作するのはとても楽しいです。皆さんもぜひ、エクセルで自分のオリジナル関数を作ってみてください。
　⇒ なんとなくの数学日記（アメショを飼ってます） 　

　cost や sint は 2*pi() ごとに同じ値を繰り返す周期関数なので、これらを組み合わせた媒介変数表示関数は閉曲線を描きます。

Excel でおにぎりとカレーパン？

　たとえば次のようなグラフです。


　媒介変数 t が動くと (x,y) は おにぎり のような形の曲線上をぐるぐる回り続けるわけです。何故おにぎりに例えるのかというと、他に思いつかなかったからです。さて、この関数を少し変形すると ......



　カレーパン のような形の曲線上をくるくる動くことになります。何故カレーパンに例えるのかというと、私の好物だからです。特に揚げたてのカレーパンの美味しさときたら「高級フランス料理だって太刀打ちできないぞ」と思ったりしています。引き続いて次のような曲線。

　

　−2π < t < 2π の範囲で描いています（ pi は円周率）。動点 (x, y) は下の方から青い矢印の方向へ移動します。今回は sint や cost に媒介変数 t が乗じられているので閉曲線にはならず、t の増加と共に原点に近づいていき、そのあと遠ざかっていきます。もう少し t の範囲を広げてみましょう。

　

　範囲は−4π < t < 4π です。矢印に沿って曲線を丁寧に目で追っていけば、軌道が螺旋を描いていることがわかると思います。

　ところで動点が最も原点に近づくときの座標はどこでしょうか？　微積分の手法を用いて原点からの距離が最小となる点と、その最小値を求めることも不可能ではないかもしれませんが、式が複雑すぎてたいていの人は途中で嫌になると思います。私は面倒なので計算する気にもなりません。エクセルを使ってラクをしましょう。原点最近接点を与える媒介変数 t と動点座標 (x, y) 、および距離 r は、


となります。もし「手計算で求めたよ！」という強者がおられたら、コメントしてください。
　⇒ なんとなくの数学日記（エクセルと数学）