���Ƃ̐��w��b�u��
�@�O�p���ƃx�N�g���� [13]�@���@�藝���܂��傤
�@�ȑO�̋L���ŒP�ʉ~��p���� sin30���� cos45���̂悤�Ȓl���v�Z���܂������ǁA���߂���l������ꂷ���Ă��āA�Ȃ��S���ƂȂ��ł��ˁB�����ł��������v�Z�͈͂��g�傷�邽�߂� ���@�藝 �Ƃ������������Ƃɂ��܂��B������g���� sin15���Ƃ��Atan75���̂悤�Ȓl�����߂邱�Ƃ��ł���悤�ɂȂ�܂��B���ς��g���ƊȒP�ɉ��@�藝�������o����Ă��܂��܂���B�܂��͉��̐}���������������ȁB�@
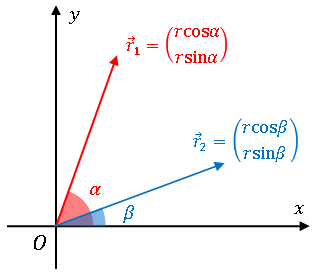
�@�����傫���ŁAx ������̊p�x��, �����Ȃ��Q�̃x�N�g��
�̓��ς𐬕��\���̌����ł����Ă݂�� ......
�@����ŁA���̂Q�̃x�N�g���̂Ȃ��p�� ���|�� �ł�����A
�Ə������Ƃ��ł���킯�ł��B�����͓��R�������͂��ł�����A
�ƂȂ��ĉ��@�藝���P�ł�������ł��I�@�c��̉��@�藝�͂��̎����瓱�����Ƃ��ł��܂���B�܂���̎��� �|�� �� �� �Ƃ����ƁAcos(�|��) = cos��, sin(�|��) = �|sin�� ���A
�Ƃ����Q�߂̉��@�藝�������܂��B���� (1) ������
�Ƃ������������܂��B�� = �� + �� �Ƃ���ƍ��ӂ�
�ƂȂ�̂ŁA
�Ƃ��������������܂��B���̎��� �|�� �� �� �Ƃ�����
�ƂȂ�܂��B�܂� (2) �� (3) ����
�@���ӂ� cos��sin�� �Ŋ����
�������܂��B����ł͎O�p���̉��@�藝���܂Ƃ߂Ă����܂���`�B
�@����ō��܂ł��F�X�ȎO�p���̒l���v�Z�ł���̂ˁ`�B
�@�Ō�ɂЂƂ��������Ă݂܂���`�Bsin75���̒l�����߂܂���B
�@�����ƌv�Z�ł��܂����ˁ`�B
�@�F������F�X�Ȓl�Ŏ����Ă݂Ă��������ȁ`�B
�@����ł͂܂�������܂���`�B
�@ �@
�@�����g�����������������Ȃ���A���w�̉��̐[�����������Ă��܂��B
���ɂȂ�܂��B