今回も微分方程式です。基本的な変数分離形で解きます。
問題51 変数分離して微分方程式を解きます [高3★★☆☆☆]
次のような微分方程式を考えます。(1) y(0) = 0 を満たす解を求めてください。
(2) y(0) = 2 を満たす解を求めてください。
(3) (1) と (2) のグラフの概形を描いてください。
[ヒント] 片方のグラフを描けば、もう1つは「折り返し」や「平行移動」で描くことができます。
≫ [おすすめ数学書籍広告] 実験数学読本
解答51(変数分離します)
まず変数分離して積分して一般解を得ます。最後に A = ±eC と任意定数を置き直しています。
(1) y(0) = 1 + A = 0 なので A = −1
この解を y = f(x) とおくと、
となります。
(2) y(0) = 1 + A = 2 なので A = 1
この解を y = g(x) とおくと、
となります。
(3) y = f(x) を微分すると
f'(x) = 0 となるのは x = 0 。
f'(−1) < 0, f'(1) > 0 なので f(0) は極小値です。
さらに y(−∞) = 1, y(+∞) = 1 です。
また g(x) = −f(x) + 2 ですから、f(x) のグラフを x 軸で上下折り返して y 軸方向に 2 を加えればよいことがわかります。以上より、グラフの概形はまとめて次のようになります。
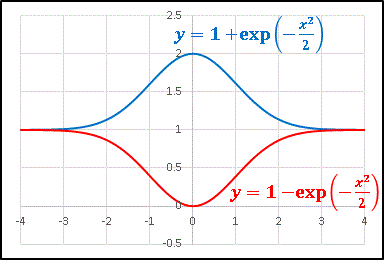
ちなみに A = 0 のとき、すなわち y = 1 も解曲線の1つであり、微分方程式を満たしていることがわかります。