�@�v���Ԃ�ɑ�w���p�̖���p�ӂ��܂����B�L���ȃt�B�{�i�b�`����̈�ʍ������߂���ł����A���`�㐔�w�̗v�f����������l�܂��Ă��܂��B��w�Ŋw���`�㐔�w�̒m������������Ɛg�ɂ��Ă��邩�m�F�������ʼn����Ă݂Ă��������B
���43�@�t�B�{�i�b�`����̈�ʍ��@[��w�Q����������]
�@�t�B�{�i�b�`����͑O�� 2 ���𑫂����킹�č�鐔��ł��B�@�@F1 = F2 = 1,�@Fn + 2 = Fn + 1 + Fn
�@���̑Q�������s��ŕ\�����A�t�B�{�i�b�`����̈�ʍ������߂Ă��������B
[�q���g] �������ł����A��b�I�Ȃ��Ƃ�ςݏグ�Ă����ΕK�������ɒH�蒅���܂��B�u�ŗL�l�����߂�v�A�u�Ίp������v�B���̂Q���|�C���g�ɂȂ�܂��B
�@
��43�i�t�B�{�i�b�`����̑Q�������s��ŕ\�����܂��j
�@�܂��͑Q�������s��ŕ\�����Ă݂܂��B�s�����p���������Ƃ̃x�N�g���̑�P������ Fn + 1 �� Fn �̐��`�����ɂȂ��Ă���悢�̂ŁA�Ƃ�����
�ƕ\���ł��܂��B���̍s��Q�����ɂ���āA
�Ə������܂��Ă����܂��B����� Fn ��
�ƕ\����܂��B�܂荡��̖��͂��̍s��� n �| 2 ����ǂ̂悤�Ɍv�Z���邩�����Ă��܂��B���̂��߂ɂ͍s���Ίp������
�Ƃ����`�ɂ��Ȃ��Ă͂Ȃ�܂���B����ƍs����E����|���Ă������Ƃɂ���� P �� P�|1 ���L�����Z������Ă����̂ŊȒP�Ɍv�Z�ł���悤�ɂȂ�̂ł��B�����Ă��� P �Ƃ͍s�� A �̌ŗL�x�N�g�������ɕ��ׂ����̂ƂȂ��Ă��܂��B���ۂɌŗL�l�ƌŗL�x�N�g�����v�Z���Ă݂�ƁA���̈Ӗ��͂����ɂ킩��܂��B�s�� A �̌ŗL��������
x2 �| x �| 1 = 0
�ł�����A�����������
��������̂ŁA
�Ə������Ƃ��ł��܂��B�Q�̌ŗL�x�N�g������ׂ�
�Ƃ����悤�ɂ܂Ƃ߂ď�����̂ŁA�E����t�s���������
�ƂȂ�̂ŁAP �͌ŗL�x�N�g������ׂ����̂ł��邱�Ƃ��킩��܂��B
�@x1 = ��y1, x2 = ��y2 �ł�����
(x1, y1) = (��, 1),�@(x2, y2) = (��, 1)
�Ƃ����ŗL�x�N�g���܂��B P �Ƃ��̋t�s���
�ƂȂ�܂��B���Ƃ�
�����ƌW���̊W
�� + �� = 1,�@�� �� = �|1
�̊W���g���Čv�Z���A�Ō�� �� �� �� �ɒl������ƁA
�������܂��B
[�⑫] �t�B�{�i�b�`����
�@�@ �P�����̃E�T�M�����܂��B�@�A �Q������ɂP�����̃E�T�M���Y�݂܂��B
�@�B �R������ɂ��Ƃ̐e�E�T�M�ƎY�܂ꂽ�E�T�M�����ꂼ��P�����̃E�T�M���Y�݂܂��B
�@
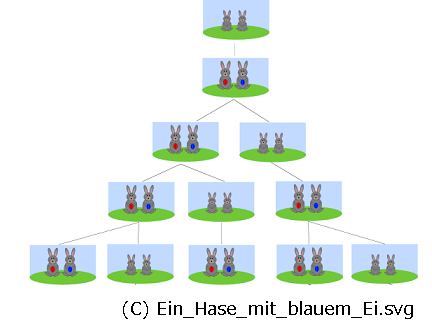
�@��������X�ƌJ��Ԃ��̂��t�B�{�i�b�`����ł��B��̓I�ɂ�
1, 1, 2, 3, 5, 8, 13, 21, ......
�Ƃ����悤�ɊȒP�ɏ������ׂĂ������Ƃ��ł��܂��i�O�̂Q�̐����𑫂��Ď��̐���������Ă��܂��j�B�t�B�{�i�b�`����͕s�v�c�Ȑ�����������������Ă���A���̐���������������łP���̖{��������قǂł��B���̃u���O�ł�����ʂ��āA���������̐����𖾂炩�ɂ��Ă��������Ǝv���Ă��܂��B
�@ �@