�@�ł͂��̕������� x �������Ă݂�� ......
���12�@�u���ϕ��Ŗʐς����߂Ĕ��~�Ɣ�r���܂� [���R����������]
�@�� f(x) �����̂悤�ɒ�`���܂��F�@��������`��� �| 1 �� x �� 1 �Ƃ��܂��B
(1) y = f(x) �̃O���t�̊T�`��`���Ă��������B
(2) y = f(x) �� x ���ɂ���Ĉ͂܂ꂽ�ʐ� S �����߂Ă��������B
(3) ���a 1 �̔��~�̖ʐς� T �Ƃ��āA(2) �ŋ��߂��ʐ� S �Ƃ̔䗦 R = S / T �����߂Ă��������B
[�q���g] (2) �̓^�C�g���ɂ���悤�Ɂu�u���ϕ��v�Ōv�Z���܂��B
�@
≫ [Amazon�������i] ���d���Z���~�b�N�R���f���T�[�i�G�R�m�~�[�Z�b�g�j
��12�i�������̐ϕ��������g���܂��j
(1) �܂��� f(x) ��������܂����A�������̐ϕ��Ɋւ��鎟�̌����͂����ւ�L�p�Ȃ̂ł��Њo���Ă����Ă��������B�@�㎮�Ɛς̔������� (fg)' = f'g + fg' ��p���� f(x) ����������
�ƂȂ�܂�����Af'(x) = 0 �Ƃ�����
x = �}��2/2
�ŋɒl f(�}��2/2) = 1/2 ���Ƃ邱�Ƃ��킩��܂��Bf(x) �͊���ł�����A�Ƃ肠���� 0 < x ��`���A���ƂŌ��_�Ώ̂ɐ܂�Ԃ��ĕ��̗̈��`�����Ƃɂ��܂��B��2/2 < 3/4 �ɒ��ӂ��ċɒl���Ƃ� x = ��2/2 �O��� f'(x) �̕����ׂ�ƁA
f'(0) > 0,�@f'(3/4) < 0
�ł�����A f(��2/2) �͋ɑ�l�ł��邱�Ƃ��킩��܂��B
�����ЂƂ��ӂ��Ă��������̂��Ax = 1 �t�߂ɂ����� f'(x) �̗l�q�ł��B
x �� 1�@�F�@f'(x) �� �|��
�ł�����A���̕t�߂ŌX���͉~�Ɠ����悤�Ɍ���Ȃ������ɋ߂Â��܂��B�ȏ�̂��Ƃ��l�����ăO���t��`���Ɖ��}�̂悤�ɂȂ�܂��B
�@

(2) ������q�ׂ��悤�ɁAf(x) �͊���ł�����A0 ���� 1 �܂Őϕ������l S/2 �����߂āA�Ō�� 2 �{���܂��B���̌`�̊���ϕ�����Ƃ��ɂ́A
x = sin��
�ƕϐ��ϊ�����̂��R�c�ł��B
�ƁF0 �� pi/2�A�@dx = cos��d��
�ł�����A�ϕ���
�̂悤�ɂȂ�܂��B���̐ϕ������s����Ƃ��́A
�@�@�@(cos3��)' = 3cos2��(�|sin��)
�@�@�@�́@(�|cos3��/3)' = cos2��sin��
�̊W���g���܂��B�v�Z����� S/2 = 1/3 �������܂��B����ē�����
S = 2/3
�ƂȂ�܂��B
(3) ���a 1 �̔��~�̖ʐ� T �͂������ pi/2 �ł�����A
R = S/T = 4pi/3
�ƂȂ�܂��B�l���v�Z����� 0.423 �ł��B
�@�Q�l�̂��߂ɔ��~�� y = g(x) ��Y�������}�����Ă��������F
�@
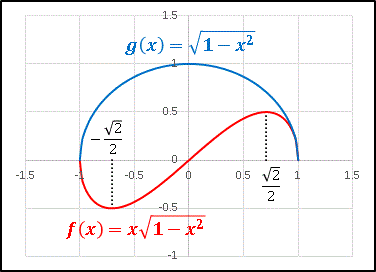
�@f(x) �� g(x) ���������ׂ��ꂽ�i�D�ɂȂ��Ă��܂��ˁB
�@|x| �� 1 �ł�����Ax ���|����Ƃ������Ƃ́A�S��Ŕ��~���̒l�������邱�ƂɂȂ�A���ʂƂ��Ėʐς������ȉ��ɂȂ��Ă��܂��܂��B
�@ �@